随机过程期末复习笔记

[toc]

---

随机过程基本概念

设$E=\{e\}$是样本空间，如果对每一个时刻$t\in T$定义在$E$上的随机变量$X(e,t)$，则称一簇随机变量$\{X(e,t),e\in E,t\in T\}$是一个随机过程。

例如，“北京一年中的气温”就是一个随机过程。

随机过程的统计描述

1. 一维分布函数： $$F_x(x,t)=P\{x(t)\le x\}$$

2. 一维概率密度： $$p_x(t)=\frac{dF}{dx}$$

3. 特征函数： $$\varphi (\omega )=E[e^{j\omega x(t)}]=\mathcal{F}[p_x(x)]$$ 若干个相互独立的随机变量$x_1\cdots x_n$的和$S=\sum x$的特征函数等于它们的特征函数的积，即： $$\varphi (\omega ;S)=\prod _{i=1}^n\varphi (\omega ;x_i)$$

随机过程的数字特征

1. 均值（期望） $$ 均值是一个时间的函数。例如对前面的随机过程“北京一年中的气温”来说，“过去若干年中每个时刻的气温的平均值”就是均值。

2. 均方值 $$

3. 方差 $$

4. 自相关函数 $$

5. 协方差 $$

几个相关概念：

1. 随机过程正交 $$ 或： $$

2. 随机过程不相关 $$

3. 随机过程统计独立 $$

独立的一定不相关，不相关的不一定独立。

如果$$，那么正交和不相关等价。

平稳随机过程

1. 严格平稳随机过程 $$

2. 宽平稳过程

   同时符合以下条件：

   1. $$是一个常数，与时间无关
   2. $$，仅和$$和$$的差有关
   3. 二阶矩$$

一般来说，严平稳和宽平稳不能互相推出（即，一个严平稳过程也不一定是宽平稳过程），但是在高斯随机过程中，二者等价。以下主要讨论宽平稳过程。

平稳随机过程的相关函数$$有以下性质：

1. $$。如果过程是实过程，那么$$是偶函数。

   证明： $$

2. $$

   证明： $$

3. $$

4. $$

相关系数和相关时间

这是和自相关函数紧密关联的两个参数。

相关系数定义为： $$ 它除去起伏量强度的影响，确切表示了关联程度。

相关时间定义为： $$ 相关时间越小，随机过程随时间变化越激烈。

时间平均和各态历经

只有平稳随机过程才讨论时间平均、时间自相关和各态历经性。

随机过程的时间平均定义为： $$ 时间自相关定义为： $$ 时间平均和时间自相关都是状态量的函数，这与期望不同。例如，北京$$年的平均气温，这是和$$有关的数字，这就是时间平均。北京各年$$时刻的平均气温，这是$$的函数，这就是期望。

如果有：

1. $$（均值各态历经）
2. $$（自相关各态历经）

则称随机过程是各态历经的。

平稳随机过程的功率谱

只有平稳随机过程才讨论功率谱。 $$ 即：功率谱和自相关函数是一对傅里叶变换对。

因为$$是偶函数，所以 $$

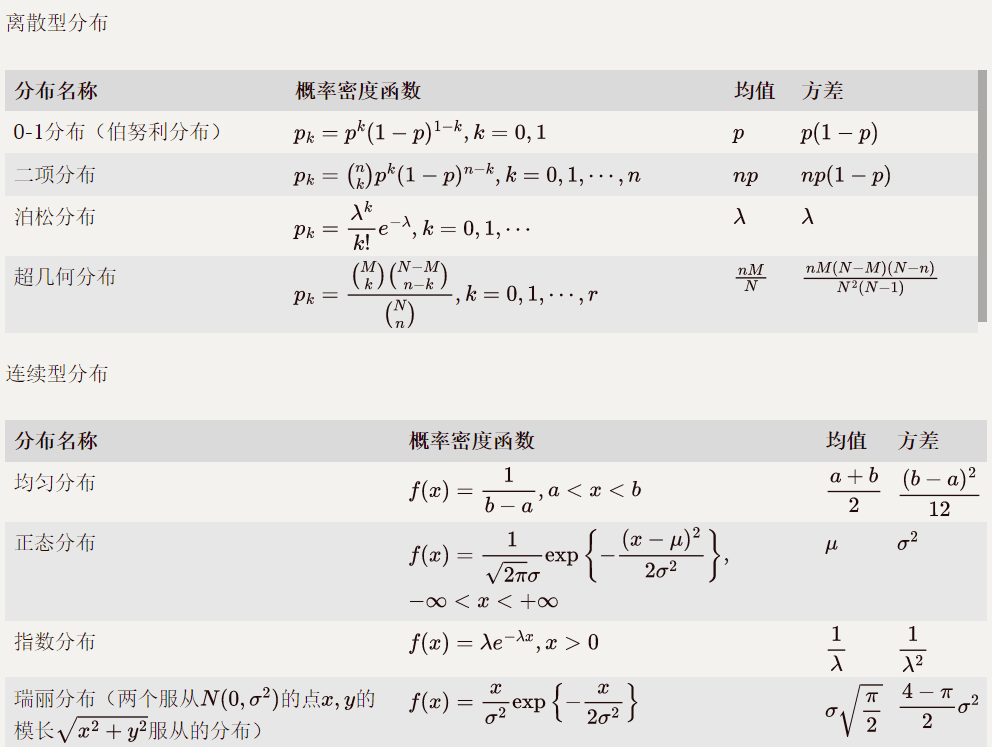
常用概率分布速查表

以下是常用概率分布的概率密度函数、均值和方差速查表：

image-20250105220758712

【例】设随机过程$$，其中$$是相互独立的，服从$$均匀分布的随机变量。

1. 求$$的均值和自相关函数，判断是否是宽平稳过程
2. 判断$$是否是均值各态历经的。

【解】

因为$$，所以 $$ 计算自相关函数： $$ 计算时间平均： $$ 故均值各态历经。

随机过程通过线性系统

设有线性系统 $$ 对于线性时不变因果系统，设 $$ 则有： $$ 记系统传递函数为： $$

均方微积分

当$$时，$$均方收敛于$$，记作： $$ 均方微积分，就是把普通微积分里面的极限都换成上面这个均方极限。下记$$为$$的均方微分过程，即： $$ 关于微分过程的性质，有：

1. $$
2. $$
3. $$
4. $$

特别的，如果$$平稳，有：

1. $$
2. $$
3. $$
4. $$
5. $$

对于均方积分过程，只需要将对变量求导换成对变量积分即可。注意到，对于平稳过程，有：$$，因此平稳过程通过线性系统以后不一定是平稳过程。

冲激响应法

即利用随机过程线性变换的冲激响应来研究经过线性变换后的随机过程的性质。有： $$ 因此：

1. $$
2. $$
3. $$
4. $$

如果$$平稳，有：

1. $$
2. $$
3. $$
4. $$

频谱法

即利用传递函数$$分析 $$ 有：

1. $$
2. $$，其中上划线表示共轭
3. $$

重要傅里叶变换

$$	$$
$$	$$
门函数（在$$为$$，其余为$$）	$$
三角形函数（在$$为$$，$$处为0，中间用直线段连接），记作$$	$$
$$	$$
$$	$$
$$	$$
$$	$$

【例】设$$是高斯白噪声过程，功率谱密度为$$，通过如图所示的线性系统，求：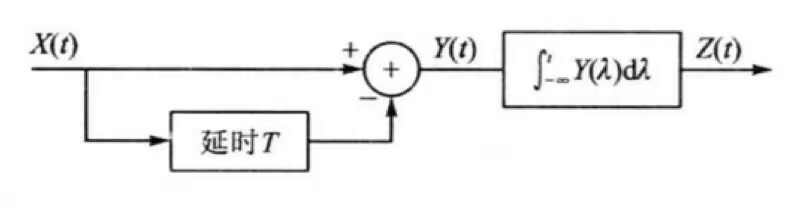

image-20250105220718243

1. $$
2. $$
3. $$

【解】

1. 求$$ $$

2. $$ $$

3. $$ $$

窄带随机过程

复随机过程

即形如 $$ 的随机过程。

关于其数字特征，有：

1. $$
2. $$
3. $$

希尔伯特变换

希尔伯特变换定义为： $$ 这个定义有三种等价写法：

1. $$
2. $$
3. $$

希尔伯特变换的性质有：

1. $$

2. $$

3. 对有限带宽信号： $$ $$，有： $$ $$ $$

4. 若$$，则 $$

5. 翻转奇偶性

实随机过程的复表示

$$

关于其数字特征，有：

1. $$
2. $$
3. $$

窄带随机过程

设有窄带随机过程

$$

则其正交表示为

$$

其中

$$

且有

$$ 窄带随机过程正交表示的统计特征

1. 自相关函数

$$

2. 互相关函数

$$ $$

$$

3. 在同一时刻 $$ ；

【例】窄带实平稳随机过程： $$ 已知$$， $$ 求：

1. $$
2. $$
3. $$

【解】

1. $$ $$

2. $$ $$ 则： $$

3. $$ $$

高斯过程

任意有限维分布都是高斯分布的随机过程叫高斯随机过程。

一维高斯分布函数： $$ $$维高斯分布函数： $$ 高斯分布的不相关可以推出相互独立（思路：协方差矩阵$$只有对角线有元素）

【例】已知 $$ 是均值为零，自相关函数为 $$ 的高斯白噪声，且有

$$

其中 $$ 为延迟时间，冲激响应函数 $$ 。求： 1．$$ 和 $$ 的互相关函数 $$ ： 2．$$ 和 $$ 的互功率谱密度 $$ ： 3．$$ 的一维和 $$ 维概率密度函数。

【解】

1. 记$$为全系统冲激响应，则： $$

2. $$ $$

3. $$ $$

泊松过程

计数过程

计数过程表示在一段时间内某事件发生的次数。计数过程的特征有：

1. $$
2. $$
3. $$

独立增量过程

$$与$$相互独立（区间不相交）。

泊松随机过程

满足以下条件的计数过程：

1. 平稳增量

2. 独立增量

3. 单跳跃：在计数随机过程中，同一时刻至多只有一个计数增量 $$

4. 随机性：在计数随机过程中，时间间隔 $$ 内出现事件 $$ 的次数为 $$ 的概率 $$是任意的，即令 $$

   且 $$

称为泊松过程。有： $$ 其数字特征为：

1. $$
2. $$
3. $$
4. $$
5. 特征函数：$$

到达时间和到达间隔

泊松计数过程第$$个到达时间$$的概率密度 $$ 泊松过程中逐次到达的时间间隔的长度$$称为到达间隔，有： $$ 所有到达间隔都服从同样的分布： $$

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：