自动控制原理（轨迹分析）

轨迹分析主要包含两部分内容，即根轨迹分析和频域分析（即奈奎斯特图和波特图）。

根轨迹分析法

闭环系统的根轨迹指的是闭环系统特征方程的根随着系统开环增益$K$从零变化到正无穷时变化的轨迹。得到根轨迹图后，就有一一对应的一组系统闭环极点分布，再考虑到系统的闭环零点分布和输入函数等，就可以完成系统的性能分析。

我们知道，稳定的充要条件就是闭环系统的极点，也就是闭环系统特征方程的根都在$s$坐标系的左半平面（也就是实部小于零），可以根据不同$K$取值对应的根轨迹位置，来观察$K$对系统稳定性的影响。

根轨迹方程和幅值相角条件

闭环系统的特征方程为： $$G(s)H(s)=-1$$ 那么我们可以写出根轨迹方程： $$K\cdot \frac{\prod _{i=1}^m(s-z_i)}{\prod _{j=1}^n(s-p_j)}=-1$$ 凡是满足根轨迹方程的$s$点都在系统的根轨迹上，其中$K$是根轨迹增益。对于每个$K$，都有一组对应的闭环极点，当$K:0\to \mathrm{\infty }$时，不同的$s$点就形成$n$条系统根轨迹（其中$n$是分母的次数）

把根轨迹方程写出幅值和相角形式，即： $$K\cdot \frac{\prod _{i=1}^m(s-z_i)}{\prod _{j=1}^n(s-p_j)}=1\mathrm{\angle }(2k+1)\pi$$ 进一步，可以写出幅值条件： $$\frac{\prod _{j=1}^n|s-p_j|}{\prod _{i=1}^m|s-z_i|}=K$$ 相角条件： $$\sum _{i=1}^m\mathrm{\angle }(s-z_i)-\sum _{j=1}^n\mathrm{\angle }(s-p_j)=(2k+1)\pi (k=0,\pm 1,\pm 2,\cdots )$$

绘制根轨迹图的基本规则

根轨迹的对称性

因为特征方程的根不是实数就是共轭复数，所以根轨迹是关于实轴对称的，所以画的时候只用画上半平面（或者下半平面）的就行了。

根轨迹的起始点和终止点

根轨迹起始于开环极点，终止于开环零点。

根轨迹的条数

对于$$阶系统，根轨迹有$$个起始点，因此有$$条。在这$$条中，有$$（零点数）条终止于有限零点，其余的终止于无穷远点（无限零点）。

根轨迹在实轴上的分布规律

对于实轴上的一段，如果其右边的开环零极点数目之和是奇数，那么这段实轴是根轨迹的一部分。

根轨迹的渐近线

有$$条根轨迹终止于无穷远点，描述它们的方法就是用渐近线。确定渐近线的方法很简单，即首先确定其斜率，然后确定其在实轴（横轴）上的截距。

其斜率（与正实轴的夹角）满足： $$ 截距（和实轴的交点）满足： $$

实轴上根轨迹的分离点和汇合点

根轨迹在实轴上的某个点分叉或者相会，这个点就称为分离点或者汇合点，而且这个点一定是重极点。算分离点和汇合点的方法有两种。

其一是解方程： $$ 得到的$$们即为分离点或汇合点。

其二是解联立方程： $$ 得到的$$即为分离点或汇合点。当然解这个方程不是硬解，因为里面有个常数$$。一般是先解下面的那个，然后检验解是不是在根轨迹上就行了。

根轨迹的起始角和终止角

起始角就是开环极点处根轨迹的切线和正实轴的夹角；终止角就是开环零点处根轨迹和正实轴的夹角。

$$极点处起始角为： $$ $$零点处终止角为： $$

根轨迹的分离角和会合角

根轨迹在$$平面上相遇后分开，分离角指的是根轨迹离开重极点处的切线和正实轴的夹角；会合角指的是根轨迹进入重极点处的切线和正实轴的夹角。有： $$

根轨迹和虚轴的交点

根轨迹最重要的部分就是在靠近虚轴和原点的那一部分，因为判定系统稳定的依据就是根是否都在$$坐标系的左半平面。

利用系统闭环特征方程，令$$代入后满足特征方程实部虚部均为零，则$$就是根轨迹和虚轴的交点 $$

【例】已知单位反馈系统开环传递函数是 $$ 画出根轨迹图。

【解】第一步：将其化成零极点形式 $$ 其中$$。系统没有开环零点，$$；有四个开环极点，$$，四个极点分别为$$。

第二步：根轨迹总共有四条，起始点分别为$$，终止点都是无穷远点。

第三步：根轨迹渐近线的实轴截距为： $$ 斜率为 $$ 取$$，得夹角为$$

第四步：求复数极点处的起始角 $$ （取$$）。则$$

第五步：求实轴上分离点坐标和分离角 $$ 解得$$，分离角为$$

第六步：求根轨迹和虚轴的交点。闭环特征方程为： $$ 令$$，代入： $$ 令实部虚部都是零，有： $$ 得$$。

于是，可以画出根轨迹图了。

根轨迹图

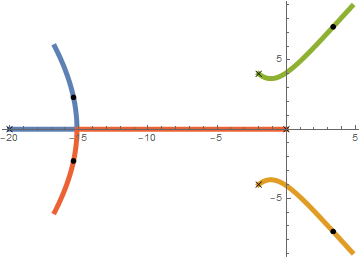
上面这张图是用Mathematica画的，代码为：

RootLocusPlot[k/(s*(0.05*s + 1)*(0.05*s*s + 0.2*s + 1)), {k, 0, 80}, 
 PlotStyle -> AbsoluteThickness[5.`]]
MATHEMATICA

频域分析法

系统的频率响应函数就是把$$里面的$$换成$$，即$$。

在进行频域分析法时，有两件事是无论如何都要注意的：

1. 对开环系统函数进行分析

2. 要把系统函数各个因子的系数化为1，即： $$

奈奎斯特图

奈奎斯特图就是在复平面上$$的值随$$从$$变化到$$时的参数图像。在介绍奈奎斯特图的画法时，我将介绍两种方法。首先介绍一种公式法，然后来说明公式法的本质。

公式法

按照下面几个步骤，可以画出奈奎斯特图。

1. 确定起点

   起点按照以下公式确定： $$ 其中$$是传递函数分母里面单个$$的指数，$$是分子上提出来的系数。

   然后，看（分母中$$一次项的系数之和-分子中$$一次项的系数之和），如果这个值大于零，那么就在前进方向的坐标轴的左侧，否则在右侧。

   以 $$ 为例，有$$，所以$$

   分母中$$的系数之和为$$，分子中$$的系数之和为零，所以在前进方向坐标轴的左侧，即正向纵轴的左侧，即从第四象限起笔

2. 确定终点

   终点按以下公式确定： $$ 其中$$是分子的总次数，$$是分母的总次数，$$，$$

   $$代表分子/分母中最小相位环节（就是$$前面系数是正的）的总阶数，$$代表分子/分母中非最小相位环节的总阶数。

   继续以上面的系统为例，分子中次数为零，最小相位环节阶数为零；分母中次数为3，最小相位环节总阶数也是3，所以 $$ 于是，知道了起点和终点，我们就可以初步画出$$的图像了：

   

   初步图像

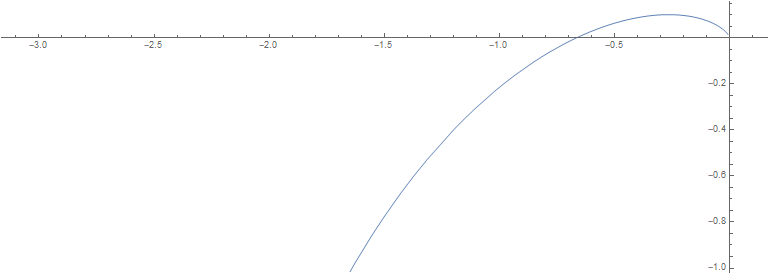
   绘图代码：

   ParametricPlot[{Re[(1)/(I*w*(I*w + 1)*(2*I*w + 1))], 
     Im[(1)/(I*w*(I*w + 1)*(2*I*w + 1))]}, {w, 0.01, 3}]
   MATHEMATICA

3. 补充虚圆

   为什么说上面的是初步呢？因为还有$$这部分的没有画，而且这部分还很重要。

   如果$$，那么不用画。

   如果$$在原点上有重根，即$$，那么以$$为开始，半径无穷大，顺时针转$$，接到上面那个图像的起点处。

   *如果$$在虚轴上有$$重共轭极点$$，则： $$ 其中$$是没有$$重共轭极点的。那么从$$开始，以半径为无穷大，顺时针转$$，接到起点处。

   还是对于上面这个例子，属于第二种情况，于是可以画出：

   

定义法

1. 确定起点

   说起起点，就是计算 $$ 不就行了吗？先来看模长部分，那当然是$$就是无穷大，因为分母是零；$$是零，因为分子是零，这是显然的。然后看相位，众所周知复数相乘就是相位相加，复数相除就是相位相减，所以相位就是分子的相位减去分母的相位之和了。考虑一个$$，当$$时，这玩意就趋向于$$，对应的相位就是$$，所以不用管，只看$$单独的那一项，一个它的相位是$$，总共有$$个它，这就是公式法里面的 $$ 的来历。

2. 确定终点

   终点就是 $$ 幅值分析略，看相位。最小相位系统就是$$，非最小相位系统就是$$，当$$的时候他俩分别就是$$，对应的相位就是$$。这就是公式法里面的 $$

3. 画出虚圆

   这里只说第二种情况。如果$$了，那么值显然是$$，实数，所以要从$$开始。但是从$$开始那它就不是实数，就有一个“确定起点”的那个角度，这时候虚圆就是把这俩连起来就行。

画图完成以后，还要计算一个点，那就是图像和横轴的交点，名叫穿越点，对应的频率叫穿越频率。

奈奎斯特稳定判据

利用奈奎斯特图判断闭环系统的稳定性，需要计算 $$ 如果$$，那么稳定。

其中，$$是开环中实部大于零的极点的个数，也可以对分母用劳斯表，看第一列的符号改变次数。

$$是曲线穿越$$这段横轴的总次数，但是有正有负：

• 虚圆穿越，总是负的
• 实线穿越，以$$作为视点，看它是顺时针（负）还是逆时针（正）
• 如果起始点、终止点在轴上，算$$次

波特图

波特图由两张半对数坐标图组成，其中一张表征幅频特征，一张表征相频特征。其横坐标是频率，为对数坐标；幅频纵坐标是dB，相频纵坐标是线性。绘制波特图首先要记住两个原则

1. 如果两个传递函数互为倒数，那么波特图关于横轴镜像对称
2. 如果两个传递函数互为共轭（即$$换成$$），那么幅频曲线相同，相频关于横轴镜像对称

然后记住两个典型环节：

1. 惯性环节 $$ 对应的幅频斜率为$$dB/十倍频，对应的相频变化量为$$

2. 震荡环节 $$ 对应的幅频斜率为$$dB/十倍频，对应的相频变化量为$$

然后可以开始画了。画的步骤如下。在下面的例子中，传递函数为： $$

1. 把系统函数按转折频率从低到高排列，并把因子写成上面的那种形式，然后在横轴上标出转折频率 $$ 所以转折频率为$$

2. 低频段（即比最低的转折频率还低的一段）：幅频斜率为$$dB/十倍频，相位起点为$$，然后根据幅频曲线一定经过$$或者$$来确定幅频曲线的位置

   在本例中，$$，$$，$$

3. 幅频图中，每段以转折频率为界限，调整斜率，在原有斜率的基础上增加目前环节对应的斜率。

4. 相频图中，每个转折频率代表相频图在$$上变化了$$，不同的转折频率之间相互叠加

5. （可选）在二阶环节对应的转折频率处补充一个高度为$$的尖峰

6. 计算幅频曲线和$$轴的交点

对数判据

要用波特图判断闭环系统的稳定性，同样要计算 $$ 其中$$是开环中实部大于零的极点的个数，$$是在$$即幅频图为正值的部分中，相频曲线穿过$$的次数之和，向上穿越算正数，向下穿越算负数

稳定裕度

稳定裕度是衡量系统相对稳定性质的量，分为相位裕度和增益裕度。

相位裕度的定义是在幅频波特图和横轴的交点$$处，使系统达到临界稳定状态的附加相移，有： $$ 在奈奎斯特图中，相位裕度$$指的是曲线和单位圆的交点和原点的连线与负实轴之间的夹角。

增益裕度$$的定义是在相频波特图和$$的交点$$处，使得系统达到临界稳定状态所需增大的增益倍数，一般用dB表示，有： $$ 在奈奎斯特图中，增益裕度是曲线和负实轴的交点离原点的距离的倒数。

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：