数字信号处理·滤波器之章

你说得对，但是《数字信号处理》是电子信息工程学院独立开设的一门核心专业课，课程发生在一个被称作D221的幻想世界，在这里，被神选中的序列将被授予“傅里叶变换”，导引频域分解之力。玩家将扮演一位名为“DSP”的神秘角色，在自由的系统中邂逅性格各异、能力独特的信号们，和他们一起分析频谱，找回失散的频段——同时，逐步发掘“线性系统”的真相。

数字滤波器设计

数字滤波器设计是通过幅频响应$|H(e^{j\omega })|$设计系统函数$H(z)$，在数字系统中编程实现。利用模拟滤波器设计数字滤波器，就是要寻求某种映射，把$s$平面映射到$z$平面，为了因果稳定性，这个映射应该满足以下两个条件：

1. $s$平面的虚轴$j\mathrm{\Omega }$映射为$z$平面的单位圆
2. $s$平面的左半平面映射为$z$平面的单位圆内

冲激响应不变法设计IIR滤波器

冲激响应不变法的根本思想是从系统的冲激响应出发，保证数字系统的冲激响应是模拟系统的冲激响应的采样，即： $$h[n]=h_c(t){|}_{t=n{T}_s}=h_c(n{T}_s)$$ 其中$T_s$是采样周期。

对模拟系统冲激响应进行理想采样，有： $$ 其拉普拉斯变换为： $$ 数字系统冲激响应的$$变换为： $$ 所以，有： $$ 把模拟信号的拉普拉斯变换在$$平面上沿着虚轴以$$为周期进行周期延拓后，按照$$，即$$的规则替换变元，即可得到$$。需要注意，和$$有关的并不是一开始的系统函数$$，而是它周期延拓后的结果$$，如果只知道系统函数，那么要么从冲激响应的路径解决问题，要么先进行周期延拓。

这个映射可以保证把$$左半平面映射到$$平面单位圆的内部，保证稳定的模拟滤波器能变换出稳定的数字滤波器。

因为上述过程中存在周期延拓，因此需要保证模拟滤波器是带限的，但是实际上这并不可能做到，因此用冲激响应不变法必定产生频域混叠。

【例】现有系统： $$ 用冲激响应不变法设计数字滤波器，求其$$

【解】对系统函数作反变换，得冲激响应： $$ 采样，得： $$ 作$$变换，得： $$

观察上例，$$处的极点变换成Z平面中$$处的极点，所以左半S平面的极点可以映射到Z平面的单位圆内；但离散时间系统函数中的零点是部分分式展开式中的极点和系数的函数，通常并不按照与极点相同的方式进行映射，因此冲激响应不变法不能保证最小相位系统映射后的仍然是最小相位系统。

双线性变换法设计IIR滤波器

为了解决冲激响应不变法的频域混叠现象，需要研究双线性变换法。双线性变换法有两步：

双线性变换法过程示意图

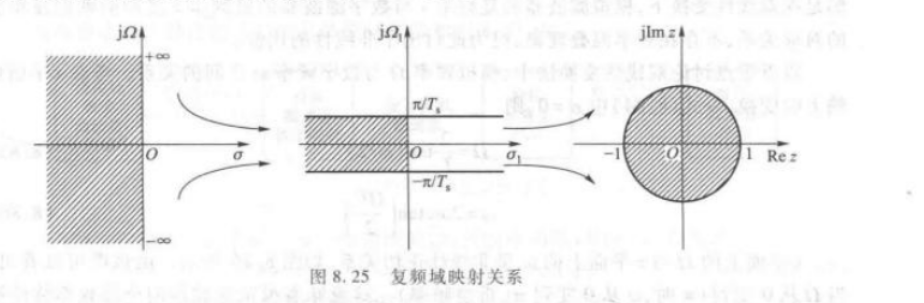
第一步，把$$平面的$$轴压缩到$$平面的$$轴$$的一段。可以通过正切变换，即： $$ 把这个关系拓展到整个$$平面，有： $$ 再通过$$变换到$$平面，有： $$ 或者说， $$ 如果$$，有： $$ 因为变换的过程中频率产生了畸变，所以设计时可以进行“预畸变”，根据 $$ 双线性变换的零极点是按照同种方式映射的，因此可以保证最小相位、全通性质在映射前后不变。而且它完全规避了频域混叠，生成的离散滤波器和连续滤波器有一一对应的关系，这一点也是和冲激响应不变法不同的。

窗函数法设计FIR滤波器

基本原理

FIR滤波器的设计任务是，选择有限长度的单位脉冲响应$$，使得系统的频响$$满足技术要求。

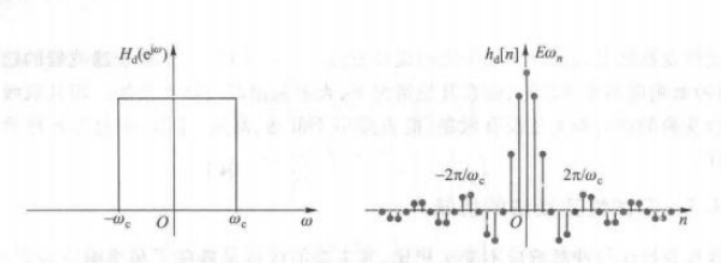
窗函数法的基本思想是，首先对理想零相位低通滤波器，画出其单位脉冲响应$$（应该是一个偶序列），如下图所示：

现在把这个$$向右移动$$位，变成$$，然后加一个窗函数$$，形成如下图所示的序列$$：

由此可见，因果可实现的FIR系统的幅度函数$$是理想滤波器的幅度函数和窗函数$$的幅度函数$$的卷积，而其相频响应来自于位移所产生的$$.有以下结论：

1. 窗函数旁瓣影响通带内波纹
2. 窗函数旁瓣影响阻带内波纹
3. 主瓣宽度影响过渡带宽度
4. 增加窗的长度可以减小主瓣宽度，从而减小过渡带，但是不能改变肩峰的相对值

常用窗函数

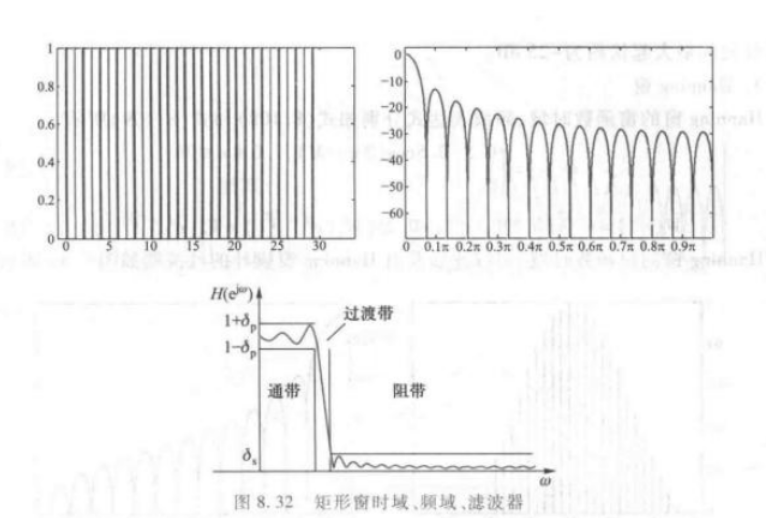
1. 矩形窗 $$

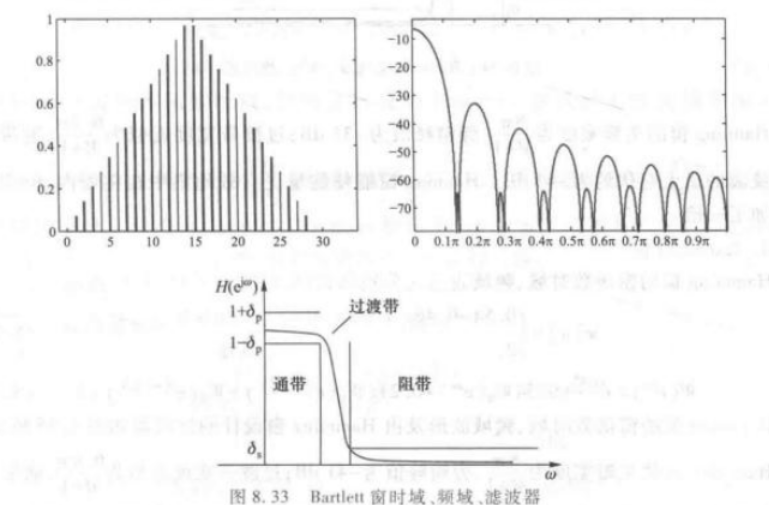
   主瓣宽度	旁瓣峰值	过渡带宽度	通带阻带波纹最大起伏
   $$	-13dB	$$	-21dB

   

2. Barlett窗 $$

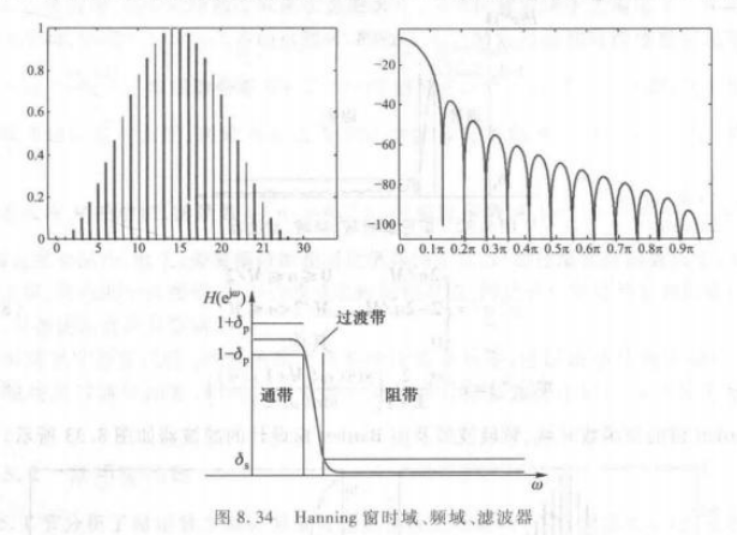
   主瓣宽度	旁瓣峰值	过渡带宽度	通带阻带波纹最大起伏
   $$	-25dB	$$	-25dB

   

3. Hanning窗 $$ | 主瓣宽度 | 旁瓣峰值 | 过渡带宽度 | 通带阻带波纹最大起伏 | | :----------------: | :------: | :------------------: | :------------------: | | $$ | -41dB | $$ | -44dB |

   

   它能使能量更有效地集中在主瓣，但主瓣更长

4. Kaiser窗 $$ 其中 $$

   $$

   $$是第一类零阶修正贝塞尔函数。于是，得到的因果滤波器为： $$ 其中 $$

频率采样法设计FIR滤波器

这个方法的思想是，根据给定的性能确定系统的频响，然后频响进行采样得到采样值$$，对其进行IDFT得到$$。具体来说，步骤如下：

1. 根据阻带最小衰减选择过渡带采样点数$$

   有$$，根据表：

   过渡带采样点数	1	2	3
   阻带衰减/dB	44-54	54-75	85-95

   选择$$

2. 确定过渡带宽度$$，根据 $$ 确定滤波器长度$$

3. 根据待设计滤波器的性能指标，确定是第几类广义线性相位系统，有以下规则：

   • $$是偶数那么在I、III中选，否则在II、IV中选
   • 第I类可做各种滤波器，第II类可做低通带通、第III类可做带通、第IV类可做高通带阻

4. 确定理想滤波器的幅频$$，相频$$

5. 对频响进行采样，对于不同的广义线性相位系统，有以下公式成立：

   1. 第I类，$$是偶数，$$ $$

   2. 第II类，M是奇数，$$ $$

   3. 第III类，M是偶数。$$ $$

   4. 第IV类，M是奇数，$$ $$

6. 求$$的$$点IDFT，得到$$

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：