北航机器学习期末考试例题汇总

本文汇总了网上可以找到的北航机器学习期末考试信息，并根据所提到的题型给出一些例题。助教说本研的课程期末考试题型基本一致，因此没有进行区分。

参考文献：

1. 北航机器学习期末考试试题2020年春
2. 北航机器学习2020-2021秋季学期期末试题回忆
3. 北航机器学习期末考试试题2019年秋
4. 北航机器学习期末考试试题2021年秋
5. 2023秋 机器学习导论 期末试题回忆版

[toc]

贝叶斯决策

【来源】参考文献3、4

【例题】细胞有正常($$)，异常($$)两类，其先验概率为$$。有一个待识别的细胞，观测值为$$，现在已知如果细胞是正常的，出现$$的概率为$$；如果细胞是异常的，出现$$的概率是$$。决策的损失表如下：

决策	$$	$$
$$	0	6
$$	1	0

1. 基于最小错误率原则对待识别细胞进行归类
2. 基于最小风险原则对待识别细胞进行归类

【解答】

1. 应用贝叶斯公式：

   已知$$，细胞属于$$的概率为： $$ 已知$$，细胞属于$$的概率为： $$ 所以，应该决策为$$。

2. 决策为$$的风险为： $$ 决策为$$的风险为： $$ 所以，应该决策为$$。

使用感知机准则求判别函数

【来源】参考文献4、5

【讲解】问题的格式是：现有样本集$$属于$$两类，寻找向量$$，使得：$$，且$$。即使用一个仿射流形把样本分成两半，这时称样本是线性可分的。其具体操作步骤是：

1. 构造规范化增广样本向量。

   这一步的关键是增广和规范化。因为一般线性流形的表达式是$$，但是我们要把这个$$包含在$$里面，就要把样本进行增广。增广的操作步骤是给样本的坐标前面补充$$个$$。

   规范化的意思是，如果样本是正例（属于$$），就保持不变；否则，它的每个坐标都变成相反数。

   规范化增广样本向量记作$$

2. 在$$集合上循环迭代：对于每个$$，计算$$，如果$$，则$$；否则，$$。直到对于某个$$，所有的$$都满足$$，那么这就是最终结果。

   这实际上是梯度下降法的过程，推导略。

【例子】现有数据集：

1. 类别1：$$，$$
2. 类别2：$$，$$

初始化权：$$，利用感知机准则求判别函数。

【解答】

1. 构造规范化增广样本向量： $$

   $$

2. 迭代

   1. $$，$$
   2. $$，$$
   3. $$，$$
   4. $$，$$
   5. $$，$$
   6. $$，$$

   至此，对于$$，所有的$$都满足$$，那么这就是最终结果。

主成分分析（PCA）数据降维方法

【来源】参考文献1、2、3、4、5

【讲解】PCA的考法有两种，第一种是基于最大方差准则进行推导，第二种是给你一些二维向量，让你降成一维。

【例题1】基于最大方差准则推导PCA的方法

【解答1】问题是把$$维数据集$$降为$$维。定义投影方向为$$维向量$$，且满足$$。

则样本均值为：$$，样本方差为 $$ 其中$$是协方差矩阵。那么优化问题为： $$ 利用拉格朗日乘数法，写出其拉格朗日函数： $$ 对$$求导，并置零，有： $$ 这意味着，$$是$$的特征值，$$是$$的特征向量。$$是$$最大特征值对应的特征向量时，方差取到极大值，称$$为第一主成分。于是，我们得到利用PCA降维的操作步骤：

1. 计算所有样本点的均值$$

2. 对所有样本点进行零均值化：$$

3. 计算协方差阵： $$

4. 计算协方差阵的最大的特征值和与其对应的特征向量$$

5. 进行投影：$$

【例题2】对以下五个二维向量，利用PCA降为一维 $$ 【解答2】

1. 计算样本均值： $$

2. 零均值化： $$

3. 计算协方差矩阵： $$

4. 计算特征值和特征向量：

   最大的特征值为$$，对应的特征向量为： $$

5. 进行投影：

   $$

【例题3】简述PCA和Fisher准则的区别

【解答3】（以下文字是AI生成的）

PCA（主成分分析）和Fisher准则（Fisher线性判别分析）都是降维技术，但它们的目标和方法有所不同：

1. 目标不同：
   • PCA：主要目的是数据压缩和特征提取，通过正交变换将数据转换到新的坐标系，使得数据的任何投影的第一大方差在第一个坐标（称为第一主成分）上，第二大方差在第二个坐标上，依此类推。PCA不涉及监督学习，即不考虑数据的标签信息。
   • Fisher准则：是一种监督学习的降维技术，目的是寻找最佳的投影方向，使得不同类别的数据在该方向上的距离尽可能远，而同类数据尽可能近。它利用了数据的类别标签信息。
2. 方法不同：
   • PCA：通过协方差矩阵的特征值和特征向量来确定主成分，选择的是数据方差最大的方向。
   • Fisher准则：通过最大化类间散度与类内散度的比值来确定最佳投影方向，选择的是区分不同类别最有效的方向。
3. 应用场景不同：
   • PCA：适用于无监督学习场景，比如数据压缩、去噪等。
   • Fisher准则：适用于监督学习场景，尤其是分类问题中的特征提取和降维。
4. 对数据的要求不同：
   • PCA：对数据的分布没有特别的要求，可以处理各种类型的数据。
   • Fisher准则：要求数据是分类的，需要知道每个数据点的类别标签。

总结来说，PCA是一种无监督的降维方法，关注于数据的方差；而Fisher准则是一种监督的降维方法，关注于类别的区分度。

支持向量机

【来源】参考文献1、2、3、4、5

【讲解】支持向量机的考法一般是让你简述一下原理，然后问一下软间隔和核函数。

【例题】svm的基本思想，模型表达式，软间隔和硬间隔的物理含义，如何用来解决非线性问题

【解答】对于分类问题：在空间中找一个超平面，最大化地分开不同数据点。对于样本$$，其中$$是空间中的点，$$是标签。找一个分类器$$，使得：

$$

SVM的思想是，寻找一个超平面，使其两端的空白区最大，即：

$$

问题等价为：

$$

这就是SVM的基本型。利用拉格朗日乘数法的对偶问题，可以写出其对偶型

$$

核技巧是应对非线性可分问题的一种方法。在$$中，如果$$不是线性可分的，则必定存在一个映射$$，使得$$在$$中是线性可分的，其中一般有$$。此时，SVM的对偶问题变为：

$$

所谓的核技巧，就是寻找一个函数$$，使得

$$

且计算$$的复杂度是$$，这样就能够加速计算。常用的核有：

1. 线性核：$$，$$
2. 多项式核：$$，$$
3. 高斯核：$$，$$

还有一种线性不可分是数据噪声造成的，这时可以用软间隔法。对于每一个样本引入一个松弛变量$$，原始问题变成：

$$

对偶问题变成：

$$

K-Means算法、EM算法

【来源】参考文献1、2、3、4、5

【讲解】一般都是考概念题，问你K均值算法、高斯混合模型、EM算法分别是什么，有什么改进空间等。

K均值算法

定义：给定 D 维空间上的数据集 $$, 这些数据对应类别未知。K均值算法将数据集划分成 $$ 类, 各类的聚类中心记为 $$, 并将每一个样本 $$ 划归到离该样本最近的聚类中心。

K均值算法的一般流程

1. 初始化选择K个初始聚类中心

2. 将每个数据点划分给最近的聚类中心 $$, 得到聚类标注 $$

3. 最小化准则函数, 重新计算聚类中心 $$。求解方法：对$$求导并置零。 $$ 求导： $$ 求解： $$

4. 迭代步骤2和3, 直到满足终止条件：聚类中心不再发生显著变化或达到最大迭代次数

高斯混合模型

是一种统计模型, 用于表示一组数据是由多个高斯分布混合而成的。具体地，高斯混合模型是多个高斯分布的线性组合，每个高斯分布称为一个混合成分, 每个混合成分都有一个对应的混合系数, 所有混合系数的和为 1

$$

GMM能够捕捉数据的多峰特性, 即数据集中可能存在多个簇, 每个簇的分布可以用一个高斯分布来描述。GMM广泛应用于聚类分析、图像分割、语音识别、数据降维等领域。

EM算法

EM算法是一种分步迭代优化算法, 适用于包含隐变量的极大似然估计问题。在高斯混合问题中, EM算法通过迭代更新隐变量 $$ 的估计值和GMM的模型参数，使得对数似然函数逐步逼近最大值。通过计算 $$ 的估计值, 可以消除隐变量的影响, 去掉 $$ 函数中的求和项 具体地，EM算法包含两个步骤。E-step：固定GMM的模型参数, 计算隐变量 $$ 的估计值, 即样本属于每个高斯分布的后验概率；M-step：已知隐变量 $$ 的估计值，通过极大似然估计更新GMM的模型参数

【例题】从$$个单高斯模型中采样，得到观测数据$$。其中第$$个单高斯模型服从分布$$，$$表示观测数据属于第$$ 个子模型的概率。请说出如何利用 EM 算法估计混合高斯模型参数，并说明得到的结果是否一定为最优解，若是，请简述理由，若不是，请简述可行的优化方法。

【解答】似然函数为： $$ 其中，$$是已知参数为$$时的正态分布概率密度函数（以$$为自变量）。

设$$为样本$$服从第$$个高斯分布的后验概率，即： $$ 将似然函数对$$分别求导，得到： $$ 则利用 EM 算法：

1. 初始化$$
2. E step:计算$$
3. M step:更新$$

最终不一定是最优解。可以初始化几次不同的参数进行迭代，取结果最好的那次。

集成学习

【来源】参考文献1、2、5

【讲解】只考过一种题。

【例题】简述集成学习的基本思想，简述Boosting和Bagging的原理和区别

【解答】集成学习的基本思想是通过多个学习器进行集成，可以获得比单一学习器更优的泛化性能。其关键是如何产生「好而不同」的个体学习器。

Boosting是串行方法，即先训练一个学习器，然后对训练集的样本分布进行调整，使得先前错分的样本的权重增加，然后以新的训练集训练新的学习器。如此重复，直到获得够多的学习器，然后进行加权组合。其特点有：

1. 弱模型、偏差高、方差低
2. 个体学习器之间有强依赖，串行生成
3. 不能显著降低方差。

Bagging是并行方法，基于自主采样法，构造$$个含$$个样本的采样集，基于每个采样集训练一个学习器。其特点有：方差低、易于并行、无法降低偏差。

决策树

【来源】参考文献1、2、3、4、5

【讲解】考法是使用ID3构造决策树，然后简述预剪枝和后剪枝法。

【例题】用ID3算法对下面的数据集进行分类，根据星球的大小和轨道判断其是否宜居：

数量	大小	轨道	是否宜居
30	大	远	是
130	大	近	是
48	小	远	是
161	小	近	是
20	大	远	否
170	大	近	否
11	小	远	否
230	小	近	否

1. 以分类目标为样本，计算总体信息熵： $$ 熵： $$

2. 计算属性：大小的信息增益：

   1. 大小-大： $$

      $$

   2. 大小-小： $$

      $$

   期望信息熵为： $$ 信息增益 $$

3. 计算属性：轨道的信息增益

   1. 轨道-近： $$

      $$

   2. 轨道-远： $$

      $$

   期望信息熵为： $$ 信息增益 $$

4. 所以，第一个结点为「轨道」：

   

   image-20241221155055706

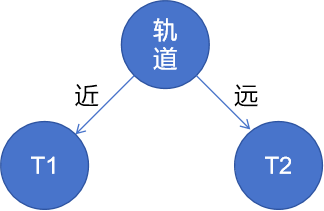
5. 计算子树T1

   因为 $$

   $$

   所以$$为叶结点，置为「不宜居」

6. 计算子树$$ $$

   $$

   所以$$为叶结点，置为「宜居」

   

   image-20241221155847215

【例题2】描述预剪枝法和后剪枝法的方法和优缺点

【解答】（以下内容由AI生成）

预剪枝法（Pre-pruning）

具体方法： 预剪枝是在决策树生成的过程中，对每个节点在划分前先进行估计，如果当前节点的划分不能带来决策树泛化性能提升，则停止划分，并将当前节点标记为叶子节点。常见的预剪枝策略包括限制树的最大深度、限制叶节点的最小样本数量、限制节点划分所需的最小信息增益等。

优点： 1. 降低过拟合风险：通过限制树的生长，减少过拟合的可能性。 2. 减少训练和测试时间：由于树的生长被提前终止，可以减少模型的训练和预测时间。

缺点： 1. 欠拟合风险：由于提前停止树的生长，可能会错过一些对模型性能有益的分支，导致模型欠拟合。 2. 视野效应问题：可能在当前划分看似不能提升性能的情况下，进一步的扩展能够显著提高性能，预剪枝会导致算法过早停止。

后剪枝法（Post-pruning）

具体方法： 后剪枝是在决策树完全生长之后进行的剪枝，它首先生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。常见的后剪枝方法包括错误率降低剪枝（REP）、悲观错误剪枝（PEP）、代价复杂度剪枝（CCP）等。

优点： 1. 泛化性能通常优于预剪枝：后剪枝保留了更多的分支，使得模型有更大的空间去学习和适应数据的复杂模式。 2. 减少欠拟合风险：相较于预剪枝，后剪枝的欠拟合风险更小。

缺点： 1. 训练时间开销大：后剪枝需要在生成完全决策树之后进行剪枝，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。 2. 计算资源需求高：由于需要在完整的决策树上进行剪枝操作，后剪枝需要更多的计算资源。

总结来说，预剪枝和后剪枝都是为了解决决策树的过拟合问题，提高模型的泛化能力。预剪枝通过提前停止树的生长来减少过拟合风险，但可能会增加欠拟合风险；而后剪枝通过在完全生成树之后进行剪枝，通常能获得更好的泛化性能，但需要更多的计算资源和时间。在实际应用中，需要根据具体的问题和数据集选择合适的剪枝策略。

概率图模型

【来源】参考文献1、2、3

【讲解】这部分的考法就是考贝叶斯网络或者马尔可夫场。先问你马尔可夫概率图的最大团，然后再让你写出两个概率图的联合分布。

其中贝叶斯网络是一个DAG（有向无环图）

贝叶斯概率图

它的联合分布就从底向上一层层写即可，如下： $$ 马尔可夫场是一个无向图，如下：

image-20241221161219707

所谓的「团」指的是任意两点之间都有边的子集。最大团指的是不能被其它团包含的团。图中的蓝色框线就是两个最大团。

马尔可夫场的联合概率分布基于最大团分解为多个因子的乘积，设所有最大团构成的集合为$$，则联合概率分布为

$$ 上图的概率分布为： $$

BP反向传播算法

【来源】参考文献1、2、3、4、5

【讲解】

首先记住这个神经元的基本结构，尤其记住各个符号的含义：

神经元的基本结构

1. $$：前一层的输入

2. $$：权值，也是神经网络训练的目标

3. $$：求和器

4. $$：求和器阈值，可有可无

5. $$： $$

6. $$：激活函数，就是ReLU啊、Sigmoid啊之类的

7. $$：神经元输出 $$

之后的神经网络图中，每一个「圆点」，其实都暗含了这些东西。

所谓的反向传播算法，就是定义一个损失函数： $$ 计算它的梯度$$，然后用梯度下降法更新$$。

算法可以分为两个阶段：

1. 前馈(正向过程)：从输入层经隐层逐层正向计算各单元的输出；
2. 学习(反向过程)：由输出误差逐层反向计算隐层各单元的误差，并用此误差修正前层的权值

image-20241221172009190

现在，我们要计算$$对$$的导数，记激活函数为$$。我们知道$$是$$的函数，$$是$$的函数，$$是$$的函数，故： $$ 现在，如果要计算$$层的梯度，即： $$

接下来使用两个记号： $$ 和 $$ 则有 $$ 因为上面已经求出了输出层的误差，根据误差反向传播的原理，当前层的误差可理解为上一层所有神经元误差的复合函数，即使用上一层的误差来表示当前层误差，并依次递推。有： $$ 其中 $$ 故： $$ 这样，我们就推导出了反向传播的递推式。

整体算法流程

1. 初始化权重 $$

2. 对于输入的训练样本, 求取每个节点输出和最终输出层的输出值

3. 对于输出层求 $$

4. 对于隐藏层求 $$

5. 求输出误差对于每个权重的梯度 $$

6. 更新权重 $$

此外，还要记住一个结论： $$ 其中$$是Sigmoid函数，即 $$

【例题1】包含一层隐藏层的前馈神经网络如图所示, 其中给定训练集 $$ 。隐藏层激活函数为 $$, 输出层激活函数为 $$ 。 $$ 表示第$$个样本 $$ 对应的神经网络输出向量, $$, 准则函数为 $$ 。网络包含$$个输入神经元, $K $$ M$个隐层神经元。试推导反向传播算法中对每一层权值参数（ $$ 与 $$ ) 的更新

image-20241228154357203

【解答1】先推导前向传播： $$ 对输出层： $$ 对隐藏层： $$ 其中， $$ 则有： $$ 则权值更新公式为： $$ 【例题2】考虑只有一个神经元的多层神经网络, 其中 $$ $$ 表示 sigmoid 函数 $$ $$, 且 $$ 。假设已知 $$, 推导 $$, 并阐述当神经网络层数过深时, 梯度消失的原因。

image-20241228162218891

【解答2】

1. $$时，有：$$，因此： $$

2. $$时，有：$$，则： $$

3. $$时，有：$$，则： $$

4. $$时，同理，有： $$

由于 $$ 且 $$, 则当层数过深时, $$ 趋于 0 , 则梯度消失

开放性试题

【来源】参考文献1、2、3、4、5

【讲解】每张卷子的最后一题是开放性试题。

【例题1】谈谈你对深度学习的理解，深度学习模型存在什么问题，你觉得深度学习未来会往什么方向发展。

【解答1】（以下解答由AI生成）

我对深度学习的理解

深度学习是机器学习的一个子领域，它基于人工神经网络的学习算法，特别是那些具有多个非线性变换的层（即深度）。这些层可以学习数据的复杂模式和表示。深度学习模型能够自动从原始数据中提取特征，而不需要人为设计特征提取算法。这种能力使得深度学习在图像识别、语音识别、自然语言处理等领域取得了革命性的进展。

深度学习模型存在的问题

1. 数据需求：深度学习模型通常需要大量的标注数据来训练，这在某些领域（如医疗图像分析）可能是不切实际的。
2. 可解释性：深度学习模型通常被认为是“黑箱”，因为它们的决策过程缺乏透明度，难以解释。
3. 计算资源：训练深度学习模型需要大量的计算资源，这可能导致成本高昂和能源消耗问题。
4. 过拟合：在有限的数据集上训练时，深度学习模型可能会过拟合，即在训练数据上表现很好，但在未见过的数据上表现差。
5. 对抗性脆弱性：深度学习模型可能对精心设计的输入（对抗性样本）非常敏感，这些输入可以导致模型做出错误的预测。
6. 泛化能力：在某些情况下，深度学习模型可能难以泛化到新的、未见过的数据或任务上。

深度学习未来的发展方向

1. 更少的数据需求：研究者正在探索如何使用更少的数据来训练有效的深度学习模型，例如通过迁移学习、元学习和数据增强技术。
2. 提高可解释性：深度学习模型的可解释性是一个活跃的研究领域，目标是使模型的决策过程更加透明和可理解。
3. 节能和效率：随着对环境影响的关注增加，研究者正在寻找更节能的算法和硬件来训练和部署深度学习模型。
4. 对抗性鲁棒性：提高模型对对抗性攻击的鲁棒性是一个重要的研究方向，以确保模型在现实世界中的可靠性。
5. 泛化能力：研究者正在探索如何提高深度学习模型的泛化能力，使其能够更好地适应新环境和任务。
6. 跨领域应用：深度学习可能会扩展到新的领域，如生物信息学、材料科学和量子计算。
7. 集成学习：结合不同的模型和算法来提高性能和鲁棒性，例如集成学习。
8. 伦理和公平性：随着深度学习在社会中应用的增加，确保模型的公平性和避免偏见成为一个重要议题。
9. 自动机器学习（AutoML）：自动化深度学习模型的设计和训练过程，使非专家也能轻松使用深度学习技术。

深度学习是一个快速发展的领域，随着技术的进步和新挑战的出现，未来的发展方向可能会不断变化。

【例题2】给出机器学习和深度学习的联系，各有什么优缺点

【解答2】（以下解答由AI生成）

机器学习和深度学习是人工智能领域中密切相关的两个概念，它们之间存在一些联系和区别。

联系

1. 基础理论：深度学习是机器学习的一个子集，它基于机器学习的一些核心概念，如模式识别和学习算法。
2. 目标：两者都旨在从数据中学习，并做出预测或决策。
3. 数据驱动：机器学习和深度学习都依赖于数据来训练模型，并通过数据改进模型的性能。
4. 特征学习：深度学习是机器学习中特征学习的一个特例，它能够自动从原始数据中提取复杂的特征。

机器学习的优点

1. 灵活性：机器学习算法（如支持向量机、决策树、随机森林等）适用于各种不同的数据类型和问题。
2. 可解释性：某些机器学习模型（如决策树）相对容易解释，有助于理解模型的决策过程。
3. 数据效率：一些机器学习算法可以在较小的数据集上训练，不需要像深度学习那样大量的数据。
4. 适应性：机器学习模型可以更容易地适应新的数据分布，尤其是在数据分布发生变化时。

机器学习的缺点

1. 特征工程：在传统的机器学习中，特征工程是一个耗时且需要专业知识的过程。
2. 模型复杂度：对于非常复杂的数据模式，机器学习模型可能难以捕捉到这些模式。
3. 泛化能力：在面对未见过的数据时，一些机器学习模型可能泛化能力不足。

深度学习的优点

1. 自动特征提取：深度学习模型能够自动从原始数据中提取特征，减少了人工特征工程的需求。
2. 处理复杂数据：深度学习特别擅长处理高维和复杂的数据，如图像、视频和语音。
3. 强大的表示能力：深度学习模型具有强大的表示能力，能够学习数据的多层次抽象。
4. 端到端学习：深度学习可以实现端到端的学习，即直接从输入到输出的映射，无需手动设计中间步骤。

深度学习的缺点

1. 数据需求：深度学习模型通常需要大量的标注数据来训练。
2. 计算资源：训练深度学习模型需要强大的计算资源，如GPU集群。
3. 可解释性：深度学习模型（尤其是大型神经网络）通常被认为是“黑箱”，难以解释其决策过程。
4. 过拟合风险：在有限的数据集上，深度学习模型可能会过拟合，导致在新数据上的性能不佳。

总的来说，机器学习和深度学习各有优势和局限，它们在不同的应用场景下可以互补。随着技术的发展，两者之间的界限越来越模糊，例如，通过集成学习和迁移学习，可以将深度学习模型的泛化能力和机器学习模型的灵活性结合起来。

【例题3】谈谈机器学习在某领域（医疗、金融、电商、交通等）的应用

【解答3】（以下解答由AI生成）

机器学习在医疗领域的应用

机器学习在医疗领域的应用非常广泛，主要包括：

1. 疾病诊断与预测：通过分析患者的病史、基因组数据等信息，机器学习模型可以提前预测某些疾病的风险，帮助医生制定个性化的预防和治疗方案。例如，谷歌的深度学习模型通过分析视网膜扫描图像，能够准确预测糖尿病视网膜病变等眼疾，其诊断准确率媲美专业医生。

2. 医学影像识别：机器学习模型能够实现对X光片、CT扫描、MRI等影像的自动分析，提高影像学诊断的准确率，降低误诊率。

3. 药物研发与筛选：机器学习能够加速新药发现与优化，通过学习化学结构、生物活性、副作用等数据，预测化合物的药效，辅助药物设计与候选分子筛选，显著缩短研发周期。

机器学习在金融领域的应用

机器学习在金融领域的应用包括：

1. 风险评估与信用评估：金融机构利用机器学习模型分析客户的历史贷款记录、还款习惯等数据，评估其信用风险并定制个性化的贷款方案。

2. 交易策略：机器学习模型在投资预测中的应用也越来越普遍，例如，量化分析师使用机器学习算法分析市场数据，识别规律，实现高频交易。

3. 欺诈检测：机器学习模型能够实时监测交易行为，识别异常模式，及时预警并拦截潜在欺诈交易。

机器学习在电商领域的应用

机器学习在电商领域的应用主要体现在：

1. 推荐系统：电商平台利用机器学习技术，根据用户的购买历史、浏览行为等构建个性化推荐模型，提升商品转化率与用户满意度。

2. 库存优化与需求预测：零售商运用机器学习预测未来销售趋势，精准管理库存水平，避免过度库存导致的资金占用与滞销风险。

机器学习在交通领域的应用

机器学习在交通领域的应用包括：

1. 交通流量预测与拥堵缓解：通过分析历史交通数据，机器学习模型可以预测未来的交通流量，帮助交通管理部门优化交通流量分配，减少交通拥堵和事故的发生。

2. 智能交通管理：机器学习技术可以用于实时监测和预测交通状况，优化交通流量分配，提高交通的效率和安全性。

3. 自动驾驶：自动驾驶汽车依托深度学习、强化学习等技术，实现环境感知、路径规划、决策控制等功能。

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：