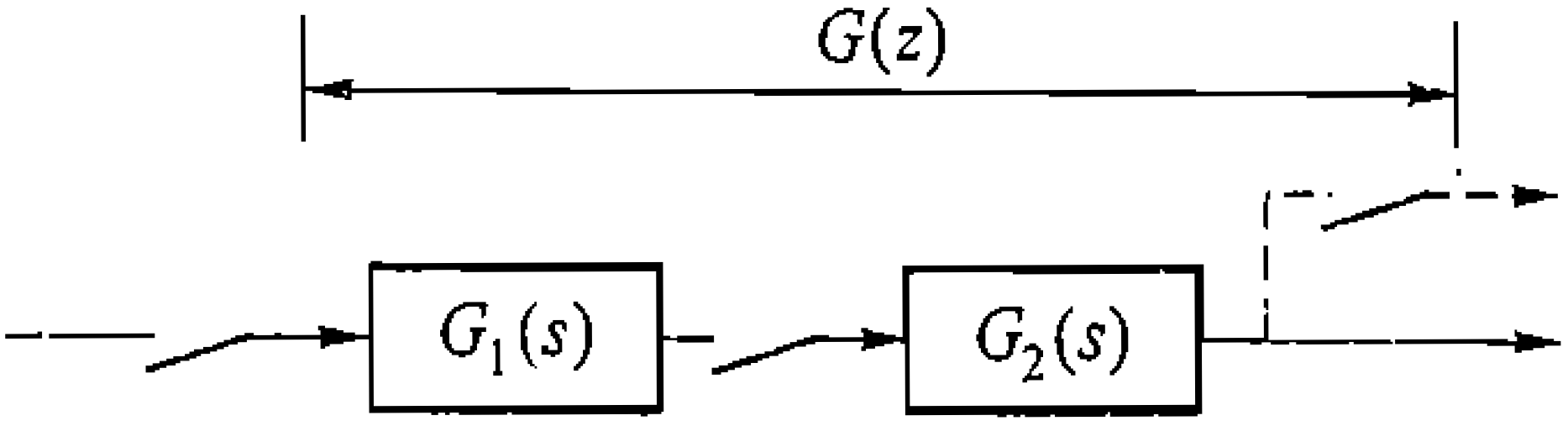
自动控制原理·采样系统和状态空间

这两部分之间其实没啥太大联系，写在一起只是为了方便，就这样。

采样系统分析

在前面讨论的系统中，信号都是连续时间信号，系统都是连续时间系统。在本节，将对有一处或者数处的信号是离散的（数码或者脉冲序列）的系统进行讨论。

关于奈奎斯特采样定理，已经提过非常非常多遍了，这里就略过了。只提一点：用$f(t),G(s)$表示采样前的信号，系统；用$f^{\ast }(t),G^{\ast }(s)$表示采样后的信号（冲击串）、系统。

保持器

由采样定理得，采样频率是输入信号频率的两倍以上时，可以通过理想低通滤波器把信号恢复出来。但是理想滤波器是不存在的，于是我们转而使用保持器来恢复信号。

• 零阶保持器

  零阶保持器是把采样时刻$nT$的采样值恒定不变地保持到下一个采样时刻$(n+1)T$的电路。它的系统函数是 $$G_h(s)=\frac{1-e^{Ts}}{s}$$

• 一阶保持器

  一阶保持器是一种按线性规律外推的保持器，其外推规律是： $$ 即：每个区间是线性函数，斜率是上一个区间的平均斜率

  其传递函数是 $$

Z变换

Z变换是拉普拉斯变换的一种变形，也学过很多遍了。

脉冲传递函数

类似于以前的系统传递函数，离散时间系统的特性可以用脉冲传递函数$$来描述。对于开环系统

image-20230617164044343

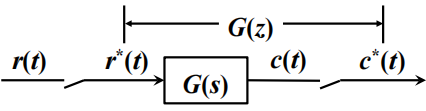
有： $$ 和 $$ 写成脉冲传递函数的形式，就是 $$ 一般来说，由连续部分求得脉冲传递函数的步骤是：

1. 由$$求得$$
2. 确定单位冲激响应序列$$
3. 求$$的Z变换，得$$

在实际操作上，并没有这么麻烦。在进行接下来的说明之前，首先要辨析两个表达式： $$ 指的是$$和$$两个表达式的乘积，两个系统之间通过采样开关串联，即：

image-20230617155047199

而 $$ 指的是先把两个连续时间系统级联，得到$$，然后求出$$对应的Z变换形式，即为$$，即：

image-20230617154959581

这两种情况一般是不一样的。比如$$，对于第一个串联系统，有： $$ 对于第二个串联系统，则有： $$ 从而 $$ 在分析闭环系统时，系统函数有时候不能直接求出（详见下面的例题），所以会转而求输出函数$$，可以遵循以下步骤：

1. 从$$开始逆着前向通道找到最靠近比较器的采样器，采样信号设为$$；
2. 利用前向通道和回路分别写出$$和$$的表达式，联立解出$$。

如果系统有多个反馈环，则：

1. 从比较器最靠近$$的回路开始，每个回路找到一个$$（没有则先归并该连续回路为一个连续环节），即$$；
2. 用前向通道写出$$的表达式，从$$依次用各回路写出$$表达式，联立$$个方程解出$$。

在实际操作时，先写$$和$$方程，再加星得到$$和$$方程，然后得到$$和$$方程.

【例1】求以下系统的$$

image-20230617164506904

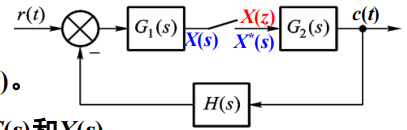
【解】$$已经在图中标好了。

1. 列方程： $$

2. 加星号（采样）：在加星号时，要分清楚一个表达式里面是系统、连续时间还是离散时间。对级联的系统、连续时间信号传入连续系统的部分合并为整体然后加星号，对离散时间信号传入系统的部分，只给系统加星号，离散时间信号保持不变，也不合并： $$

3. Z变换，就是把星号都去了，然后把$$换成$$ $$

4. 消元求解，有： $$

可以看出，在上面这个例子中，$$的存在形式是$$，并不能单独分出来，所以只能求到$$，而不能求出系统函数。

系统稳定性判定

采样系统稳定的充要条件是闭环系统的特征根全部都在$$平面的单位圆内，即$$。为了复用以前的劳斯判据，需要找到一个变换$$，把$$屏幕的单位圆映射到$$平面的虚轴之左。有： $$ 在应用时，把特征方程的$$全都替换成这个，然后对$$使用劳斯判据即可。

系统的稳态误差

首先我们研究的是稳态误差，所以系统首先要有稳态，也就是稳定。所有不讨论稳定性而直接对稳态误差进行讨论的都没有意义。

则根据终值定理，系统稳态误差为 $$ 如果是阶跃输入，即$$，则 $$ 如果是斜坡输入，$$，则 $$ 如果是加速输入，$$，$$，则 $$

总结如下：

输入	0	I	II	III	静态误差系数
$$	$$	$$	$$	$$	$$
$$	$$	$$	$$	$$	$$
$$	$$	$$	$$	$$	$$

型别指$$分母包含$$因子的个数，即$$处极点的个数

【例】对采样周期$$的系统 $$ 求输入为$$时的稳态误差

【解】有： $$ 其中$$，而 $$ 所以稳态误差为 $$

状态空间分析方法

状态空间分析方法是一种和前面讲的所有方法都不一样的方法。用传递函数描述系统只能反映系统输出和输入变量的关系，而不了解系统内部的变化情况，而且是建立在零初始状态的基础上的。而状态空间分析方法会客服这些困难。在介绍状态空间分析法前，需要定义：

• 状态变量：如果以最少的$$个变量$$就能完整描述一个系统的行为，这$$个变量就称为一组状态变量

• 状态向量：把上面这$$个状态变量拼成一个列向量，就叫做状态向量

• 状态空间：以各状态变量为轴的空间是状态空间，状态向量是状态空间里的一个点

• 状态方程：描述状态变量和输入之间关系的一阶微分方程组： $$ 其中$$是状态向量，$$是$$维输入向量，$$是$$矩阵，叫系统矩阵，$$是$$矩阵，叫输入控制阵

• 输出方程：描述系统输出和输入之间关系的方程组： $$ 其中$$是$$维输出向量，$$是$$输出矩阵，$$是$$矩阵。一个线性时不变系统可用$$直接描述。

求解系统状态方程和输出方程

对状态方程左右两边做拉普拉斯变换，有： $$ 化简一下： $$ 设预解矩阵 $$ 所以系统的特征方程为$$。则 $$ 同理，对输出方程有： $$ 如果是零状态，则$$在这里就起到了传递函数的作用，所以定义传递函数矩阵： $$

可控和可观

概念和基本判别方法

对于任意初始状态，如果存在一个控制量能在有限时刻将状态转译为零状态，则称系统状态可控。定义系统可控性阵为： $$ 如果有$$，即$$满秩，那么系统可控。

如果$$已知，能由一段时间内的输出测量值唯一确定任意时刻的状态，称为系统可控。定义系统可控性阵为 $$ 如果它是满秩的，那么系统可观。

标准型

如果一个$$阶单输入系统可控，则一定存在一个可逆线性变换，将其变为可控标准型。系统的可控标准型为： $$ 此时，对应的系统函数为： $$ 类似的，有可观测标准型： $$ 对应的单输入单输出系统传递函数： $$ 把一个系统的一般形式化成可控标准型，遵循以下步骤：

1. 计算可控性矩阵$$

2. 计算$$，记其最后一行为$$

3. 构造矩阵$$，并求逆 $$

4. 得$$

【例】把以下系统化为可控标准型 $$ 【解】有： $$ 得 $$ 求逆，有： $$ 取最后一行： $$ 所以 $$ 所以 $$

状态反馈和极点配置

对于定常系统 $$ 如果系统的输入$$和$$有关系，即 $$ 这就叫做状态反馈系统。

对于系统$$来说，其极点为特征方程$$的根，如果系统不能达到设计指标，那么就需要修改系统的极点的位置，可以适当选取状态反馈变量$$，使得状态反馈系统的特征方程$$的根满足性能要求。这样的过程就是极点配置过程。

只有系统$$完全可控时，才能进行极点配置。

【例】系统 $$ 的状态转移矩阵 $$

1. 求$$
2. 计算传递函数，写出可控标准型
3. 设$$，考虑状态反馈$$，设计$$使得闭环系统极点为$$

【解】

1. 做拉普拉斯变换，有： $$ 由$$，先求$$: $$ 所以 $$

2. 传递函数(法1) $$ 即 $$ 所以 $$

3. 有： $$ 要达到题设要求的极点，则要求特征方程为 $$ 对比系数，解方程，得 $$

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：