通信原理·数字信号基带传输

在之前的调制部分，我们解决了信号的调制和编码的问题。接下来，我们将对数字信号如何在信道中更高效地传输的问题进行讨论。

传输分为两种，即基带传输和通带传输。基带传输无需进行进一步调制，只需要直接在信道中传输编码后的数字脉冲信号（即01串方波），一般多用于非带限信道，有线传输。

通带传输需要借调制进行频谱搬移，用于带限信道，一般是无线传输，但是也可以用于有线传输，比如DVB-C。

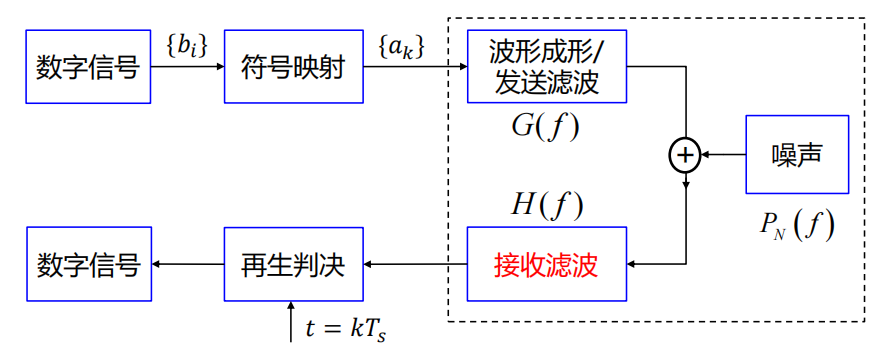
数字信号传输的方框图如下：

数字信号传输方框图

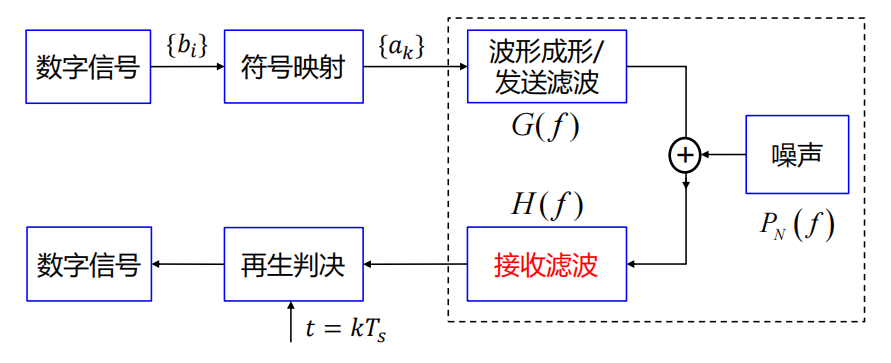
非带限信道码型设计

码型设计是数字信息的电脉冲表示过程，其主要目的是使数字信息变换为适合于给定信道传输特性的频谱结构。其设计的基本原则有：

• 尽量避免含有直流分量

• 码型变换过程应对任何信源具有透明性，和信源的统计特性无关

• 便于从基带信号中提取定时信息

• 具有检错能力

• 无误码扩散现象

• 当采用分组形式的传递码型时（如5B6B、4B3T码等），在接收端不但要从基带信号中提取位定时信息，

  而且要恢复出分组同步信息，以便将收到的信号正确地划分成固定长度的码组

• 减少基带信号中的高频分量

• 编译码设备简单

二元码

二元码的意思就是基带信号的幅度取值只有两种电平。常用的二元码有：

• 单极性非归零码：

  两个电平分别为1和0，传完一个符号后不归零

• 双极性非归零码：

  两个电平分别为1和-1，传完一个符号后不归零

• 单极性归零码：

  两个电平分别为1和0，每个符号前一半时间传输码，后一半时间归零

• 差分码：

  差分码的传输依赖于当前符号和前一个符号的变化关系。

  • 传号差分码：电平从0开始，如果当前符号是1就翻转电平，如果是0则保持电平
  • 空号差分码：电平从0开始，如果当前符号是0就翻转电平，如果是1则保持电平

各二元码的时域波形示例如下：

image-20230524104926672

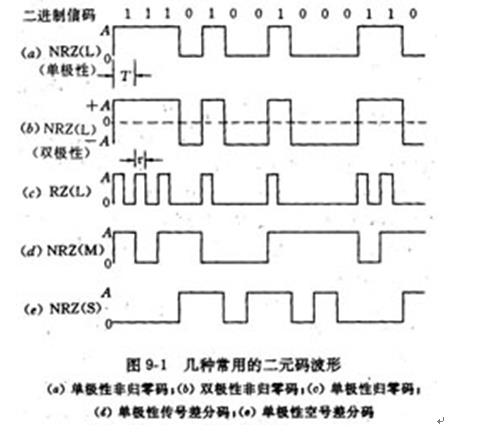
其中非差分码的低频分量丰富，不适用于交流耦合的有线信道；非归零码的连续符号不适合提取定时信息；不具备检错能力；仅适用于近距离传输。

还有一些更高级的二元码：

• 数字双相码（曼彻斯特码）

  其特点是1和0的波形反向。生成方法是用单极性非归零码和时钟信号做模二和。

• 信号反转码

  1交替用确定相位的方波（11,00）表示，0用01表示

  方便提取定时信息，有检错能力

• 米勒码

  1在码元中间跳变；单0不跳变；多个0在从第2个0起始跳变

高级二元码

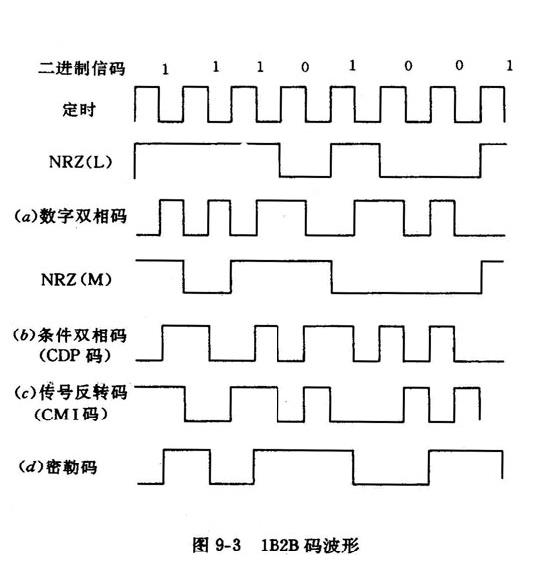
三元码

在三元码数字基带信号中，信号幅度取值有三个：+1、0、-1。

• AMI码

  其实就是符号1交替变换为+1、-1的双极性归零码。

  AMI码具有检错能力，其性能和信源的统计特性关系很密切，如果长时间出现连续0，会对定时提取造成困难。所以，使用AMI码前需要进行随机化操作，以使1、0出现的概率一致。

• HDBn码

  为了改进AMI码，提出HDBn码的概念。HDBn码是$$阶高密度双极性码的缩写，在HDBn码中信息1也交替地变换为+1与-1的归零码，但与AMI码不同的是：HDBn码中的连0数被限制为小于或等于$$。

  当信息中出现$$个连0码时就用特定码组来取代，这种特定码组称为取代节。为了在接收端识别

  出取代节，人为地在取代节中设置“破坏点”，在这些“破坏点”处传号极性交替规律受到破坏。

  一般来说，用的最广泛的是HDB3码。其生成步骤如下：

  • 加V：检查4连0的情况，如果出现，将4连0编为一组，用V取代0000的最后一个0，变成000V
  • 加B：检查相邻的V中间非零符号的个数，如果是奇数，那么记为000V，如果是偶数，则记为B00V
  • 对信码加符号：将1和B看做整体，保证这个整体按正负交替的规律变化。此时可把B恢复为1或-1
  • 对V加符号：保证V和其前一个信码的符号一致。此时可把V恢复为1或-1

  【例】将信息0100001100000101进行HDB3编码。

  【解】编码步骤如下：

  1. 加V：01 000V 11 000V 0101
  2. 加B：01 000V 11 B00V 0101
  3. 对信码加符号：0 +1 000V -1 +1 -100V 0 +1 0 -1
  4. 对V加符号：0 +1 000 +1 -1 +1 -1 00 -1 0 +1 0 -1

符号映射与波形设计

数字通信中，所需传输的往往是一个比特流，因此就需要一个符号序列去承载这个比特流。我们让这些符号在时间轴上，以$$为间隔均匀的排布，因此将其称为符号间隔/符号周期。由此，可定义符号速率为：$$。数字通信的比特速率为：$$，其中$$是数字通信的符号进制，就常用的二进制而言，符号速率等于比特速率。

比特需要转换为符号，这个过程称为符号映射。但是符号作为离散时间、离散幅度信号，不能直接传输，需要转换为连续时间、连续幅度的信号，一般是转换成准方波。这个过程叫做波形设计。

数字通信波形的统一数学表达式为： $$ 其中 $$​称为成型脉冲，将离散的符号映射为通信波形。每一个符号周期内，以$$为幅度，独立产生一个成形脉冲；并将所有符号周期形成的脉冲进行叠加，得到最终的波形。如果$$是矩形窗函数，那么就会得到一个方波，也就是之前非带限信道传输中的波形。

但是矩形窗函数是频域无限宽的信号，因此不能在带限信道中使用。带限信道中只能通过频域有限宽，时域无限宽的信号，那么既然时域无限宽，就有可能出现码间串扰。只有经过特别设计的$$才没有码间串扰，比如之前采样定理中用到的信号核重建函数 $$ 如果信号经传输后整个波形发生了变化，但只要其特定点的抽样值保持不变，那么用再次抽样的方法仍然可以准确无误地恢复原始信码。于是，有采样点无失真定理（也叫奈奎斯特第一准则）：

数字通信波形满足采样点无失真，即：$$，当且仅当： $$ 即以$$为周期对其频谱进行延拓，其和为常数。

在验证时，一般将其频域响应$$按照$$为单位进行分段，然后把各分段都沿横轴的方向平移到$$之间，并把它们叠加起来。如果实部是常数，虚部是零，那么就符合条件。

验证示意图

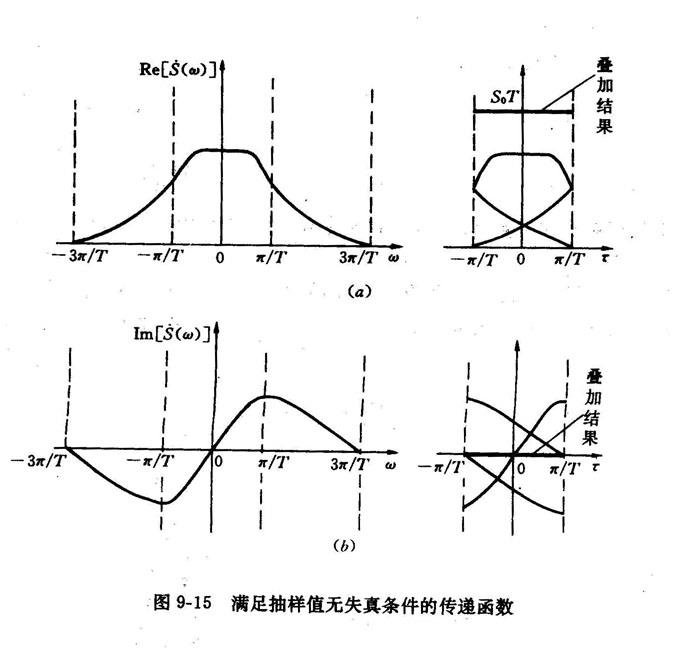
更进一步，只需验证其频域函数是否以$$为中心互补对称即可。

频谱效率指的是单位频谱上所承载的通信速率，即 $$ 由奈奎斯特第一准则知，频谱效率有上界，即 $$

升余弦成形滤波器

理想低通滤波器是最好的，可是无法实现。在实际工程中，我们一般使用升余弦成型滤波器。其频域表达式为： $$ 可以看出：它是一个偶对称的函数，其下降沿起始于$$，终止于$$，带宽为 $$ 上面的式子太抽象了，看个图就清楚了：

升余弦滤波器

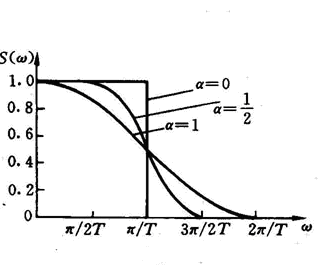
直观来说，滚降系数$$给出了下降沿的相对陡峭程度，其越小，下降沿越陡峭，频谱效率越高，物理上越难实现。一般不使用$$的升余弦滤波器。

最佳接收与匹配滤波

在之前，我们假设了接收到的信号就是发射的信号，即信道的响应是$$​。但是实际上，接收机前端会引入高斯白噪声，必须进行滤波处理，否则有大量带外噪声引入，影响通信质量。

在分析噪声时，因为主要的噪声来源是接收机本身的热噪声，所以采取加性高斯白噪声模型。其双边功率谱为： $$ 此时，考虑传输一个符号$$，成形脉冲是$$，那么我们能够观测和处理的信号是 $$ 最直接想到的方法就是在$$的最高点进行直接采样，但是这并不是最优的，因为这是因为信号能量遍布整个$$的非零区域。最佳的接受方案应该是尽可能的接收$$的能量，同时尽可能不接受$$的能量。我们可以用一个权函数$$对信号$$进行加权，然后进行积分，即： $$ 于是我们的问题就变成了怎么设计这个$$。有定理：

当且仅当$$时，信噪比 $$ 取得最大值，为： $$

【例】证明上面这个定理。

【解】从函数空间的角度来看，$$是白噪声，在各个方向上均匀分布，因此和任何方向的函数做内积，结果输出的平均能量都是相同的。有： $$ 于是，问题变成了求 $$ 的最大值的问题。也即，给定函数$$的2-范数为1，最大化$$^[1]，那么显然当$$和$$在函数空间中同方向时，这个内积最大。严格来说，根据柯西-施瓦茨不等式 $$ 有： $$ 证毕。

于是，最佳接收的系统框图为：

最佳接收系统框图

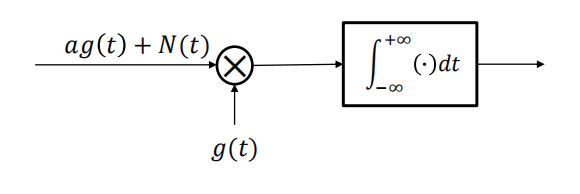
我们可将此过程等效为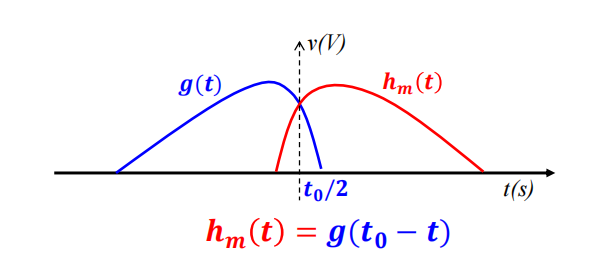$$通过一个线性系统，并对输出在$$时刻进行采样。因为上面这个线性系统蕴含了“匹配”的思想，因此被称为“匹配滤波器”。其冲激响应为： $$

匹配滤波器和发送滤波器响应镜像对称

匹配滤波器的信噪比分析

如果从一般的视角来分析匹配滤波器的信噪比增益，我们会发现是无穷大，因为$$​中噪声的功率是无穷大（因为功率谱密度是常数），因此它的信噪比是零，但是这显然没有什么意义。为了方便分析，我们将匹配滤波器等效为它本身与和它本身带宽相等理想低通滤波器的串联系统：

匹配滤波器信噪比增益计算模型

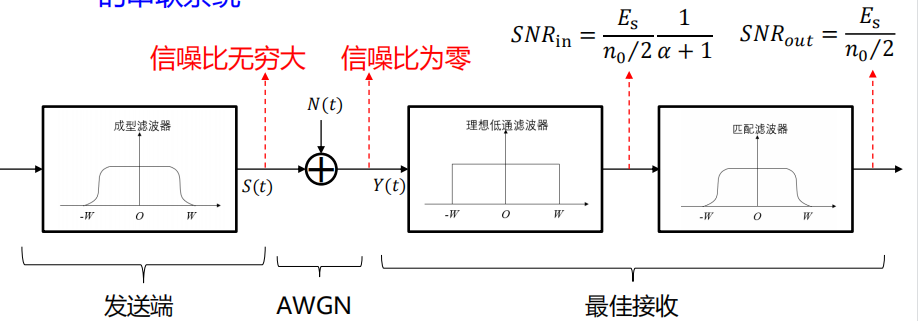
记匹配滤波器、成形滤波器和理想低通滤波器的带宽都是$$，然后可以用理想低通滤波器作为基准，来分析匹配滤波器对信噪比的增益。

$$通过理想滤波器以后，噪声的功率就被限制在了$$，注意到$$是一个符号的能量，而符号的速率是$$，所以信噪比为： $$ 由前面的分析，匹配滤波后的信噪比是： $$ 于是得到匹配滤波的增益是： $$ 可以看到：频谱效率越低，匹配滤波的信噪比增益越高。如果采取升余弦波形，那么它的增益和滚降系数有关，即： $$

根号奈奎斯特准则

在上述讨论中，我们仅仅传输了一个符号，而数字通信需要源源不断的传输间隔为$$的符号序列。此时，系统设计需要同时满足以下两个条件:

1. 采样点无失真
2. 采样点信噪比最大

回顾一下数字信号传输的框图：

数字信号传输方框图

实际上，我们需要让$$满足奈奎斯特第一准则。

因为匹配滤波器的频响是$$，所以有： $$ 那么只需要这个等效的频响函数满足奈奎斯特第一准则，就能同时满足采样点无失真和采样点信噪比最大了。有： $$ 这叫根号奈奎斯特准则。

特别的，对于升余弦滤波器来说，如果$$是升余弦滤波器，那么$$叫做“根升余弦滤波器”。

等效基带模型

为了对前两节（即应用根号奈奎斯特准则）的基带调制解调系统进行一个总体抽象，我们来看一下经过匹配滤波后$$时刻的采样值： $$ 等号两边同时除以$$，并令： $$ 则有： $$ 其中$$符合高斯分布，均值为$$，方差为 $$ 我们希望符号$$越大越好，但是发射机的平均功率有限制。其功率为： $$ 即每个符号的能量乘以单位时间内传输符号的数目。有： $$ 令$$，则$$的取值满足： $$ 在等效基带模型中，$$，$$，噪声能量$$，平均信噪比$$。

最佳判决与差错概率

回忆一下等效基带模型： $$ 观察到的是有噪声/干扰信号$$，需要根据观测值推断发送的符号$$，该过程称为判决。其中噪声满足$$，符号满足$$。

注意到$$的分布是整个实数域，而符号集合是一个离散的有限集合，所以符号判决的规范表达式为： $$ 显然这是一个多对一的映射，其实和量化挺像的。

各种判决准则

判决的根本目标是最小化错判概率，即： $$

1. 极大似然准则

   极大似然准则的基本思想是在众多的$$中寻找一个$$，使得当发射的符号是$$时接收端观察到$$的可能性最大。即： $$

2. 最小距离准则

   基于通信信号的收发关系模型$$，我们可以对ML准则做进一步的简化，得到最小距离准则 $$ 也就是选择和$$距离最近的$$。

   把相邻两个许用符号的中点称作“判决门限”，把各个判决门限中间的区域称为“判决域”。

M元ASK星座

符号集合$$直观地被称为星座图，对其的设计在数字通信中又被称为星座设计。在一维空间上，最佳的$$元星座是零均值、等概分布的，这样可以使得平均差错概率最小化。

双极性ASK星座可以表示为： $$ 其中符号半间隔为 $$

数字基带传输的差错分析方法

首先来点基础知识：标准正态截尾分布函数 $$ 这是把标准整体分布函数从一个点$$开始往后作积分，也就是一个符合标准正态分布的变量大于$$的概率。

以前面的“双极性ASK星座”为例，进行分析。

第一步，对于在两边的星座点$$和$$来说，以$$为例，当噪声$$时，$$，此时就会产生误判。于是条件差错概率为： $$ 针对任何概率形式，我们都需要将其标准正态变量(也就是$$)的统计函数，在上式中，令$$，则有： $$ 对于在中间的星座点，如果噪声$$取值过大（$$）或者过小（$$），都会出错，所以出错的概率为： $$ 第二步，综合一下，就得到平均误符号率： $$ 第三步，计算$$和$$之间的关系，有： $$ 于是 $$ 代入，有： $$ 然后计算误比特率BER，一般来说，比特和符号之间的映射采用格雷码，信噪比较高时有： $$

---

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

1. 本文中，所有省略了积分上下界的积分，都表示积分是从负无穷到正无穷。 ↩︎