自动控制原理(轨迹分析)
轨迹分析主要包含两部分内容,即根轨迹分析和频域分析(即奈奎斯特图和波特图)。
根轨迹分析法
闭环系统的根轨迹指的是闭环系统特征方程的根随着系统开环增益\(K\)从零变化到正无穷时变化的轨迹。得到根轨迹图后,就有一一对应的一组系统闭环极点分布,再考虑到系统的闭环零点分布和输入函数等,就可以完成系统的性能分析。
我们知道,稳定的充要条件就是闭环系统的极点,也就是闭环系统特征方程的根都在\(s\)坐标系的左半平面(也就是实部小于零),可以根据不同\(K\)取值对应的根轨迹位置,来观察\(K\)对系统稳定性的影响。
根轨迹方程和幅值相角条件
闭环系统的特征方程为: \[ G(s)H(s)=-1 \] 那么我们可以写出根轨迹方程: \[ K \cdot \frac{\prod_{i=1}^m\left(s-z_i\right)}{\prod_{j=1}^n\left(s-p_j\right)}=-1 \] 凡是满足根轨迹方程的\(s\)点都在系统的根轨迹上,其中\(K\)是根轨迹增益。对于每个\(K\),都有一组对应的闭环极点,当\(K:0\to \infty\)时,不同的\(s\)点就形成\(n\)条系统根轨迹(其中\(n\)是分母的次数)
把根轨迹方程写出幅值和相角形式,即: \[ K \cdot \frac{\prod_{i=1}^m\left(s-z_i\right)}{\prod_{j=1}^n\left(s-p_j\right)}=1\angle (2k+1)\pi \] 进一步,可以写出幅值条件: \[ \frac{\prod_{j=1}^n\left|s-p_j\right|}{\prod_{i=1}^m\left|s-z_i\right|}=K \] 相角条件: \[ \sum_{i=1}^m \angle (s-z_i)-\sum_{j=1}^n \angle (s-p_j)=(2 k+1) \pi \quad(k=0, \pm 1, \pm 2, \cdots) \]
绘制根轨迹图的基本规则
根轨迹的对称性
因为特征方程的根不是实数就是共轭复数,所以根轨迹是关于实轴对称的,所以画的时候只用画上半平面(或者下半平面)的就行了。
根轨迹的起始点和终止点
根轨迹起始于开环极点,终止于开环零点。
根轨迹的条数
对于\(n\)阶系统,根轨迹有\(n\)个起始点,因此有\(n\)条。在这\(n\)条中,有\(m\)(零点数)条终止于有限零点,其余的终止于无穷远点(无限零点)。
根轨迹在实轴上的分布规律
对于实轴上的一段,如果其右边的开环零极点数目之和是奇数,那么这段实轴是根轨迹的一部分。
根轨迹的渐近线
有\((n-m)\)条根轨迹终止于无穷远点,描述它们的方法就是用渐近线。确定渐近线的方法很简单,即首先确定其斜率,然后确定其在实轴(横轴)上的截距。
其斜率(与正实轴的夹角)满足: \[ \varphi_{\mathrm{A}}=\frac{ \pm(2 k+1) \pi}{n-m} \quad(k=0,1,2, \cdots) \] 截距(和实轴的交点)满足: \[ \sigma_{\mathrm{A}}=\frac{\sum_{j=1}^n p_j-\sum_{i=1}^m z_i}{(n-m)} \]
实轴上根轨迹的分离点和汇合点
根轨迹在实轴上的某个点分叉或者相会,这个点就称为分离点或者汇合点,而且这个点一定是重极点。算分离点和汇合点的方法有两种。
其一是解方程: \[ \sum_{i=1}^m \frac{1}{\sigma_{\mathrm{B}}-z_i}=\sum_{j=1}^n \frac{1}{\sigma_{\mathrm{B}}-p_j} \] 得到的\(\sigma_b\)们即为分离点或汇合点。
其二是解联立方程: \[ \begin{cases} & 1+G(s) H(s)=0 \\ & \frac{\mathrm{d}}{\mathrm{d} s}[G(s) H(s)]=0 \end{cases} \] 得到的\(s\)即为分离点或汇合点。当然解这个方程不是硬解,因为里面有个常数\(K\)。一般是先解下面的那个,然后检验解是不是在根轨迹上就行了。
根轨迹的起始角和终止角
起始角就是开环极点处根轨迹的切线和正实轴的夹角;终止角就是开环零点处根轨迹和正实轴的夹角。
\(p_1\)极点处起始角为: \[ \theta_{p1}=\pm (2k+1)\pi+\sum_{i=1}^m\angle (p_1-z_i)-\sum_{j=2}^n \angle(p_1-p_j) \] \(z_1\)零点处终止角为: \[ \theta_{z1}=\pm (2k+1)\pi+\sum_{i=1}^n\angle (z_1-p_i)-\sum_{j=2}^m \angle(z_1-z_j) \]
根轨迹的分离角和会合角
根轨迹在\(s\)平面上相遇后分开,分离角指的是根轨迹离开重极点处的切线和正实轴的夹角;会合角指的是根轨迹进入重极点处的切线和正实轴的夹角。有: \[ \theta = \frac{360^\circ}{q} \]
根轨迹和虚轴的交点
根轨迹最重要的部分就是在靠近虚轴和原点的那一部分,因为判定系统稳定的依据就是根是否都在\(s\)坐标系的左半平面。
利用系统闭环特征方程,令\(s=j\omega\)代入后满足特征方程实部虚部均为零,则\(\omega\)就是根轨迹和虚轴的交点 \[ 1+G(s)H(s)=0 \]
【例】已知单位反馈系统开环传递函数是 \[ \frac{k}{s (0.05 s+1) (0.05 s^2+0.2 s+1)} \] 画出根轨迹图。
【解】第一步:将其化成零极点形式 \[ G(s)=\frac{K}{s(s+20)(s+2+4j)(s+2-4j)} \] 其中\(K=400k\)。系统没有开环零点,\(m=0\);有四个开环极点,\(n=4\),四个极点分别为\(p_0=0,p_2=20,p_3=-2+4j,p_4=-2-4j\)。
第二步:根轨迹总共有四条,起始点分别为\(p_{1,2,3,4}\),终止点都是无穷远点。
第三步:根轨迹渐近线的实轴截距为: \[ \sigma_{\mathrm{A}}=\frac{\sum_{j=1}^n p_j-\sum_{i=1}^m z_i}{(n-m)}=-6 \] 斜率为 \[ \varphi_{\mathrm{A}}=\frac{ \pm(2 k+1) \pi}{4} \] 取\(k=0,1\),得夹角为\(\pm 45^\circ,\pm135^\circ\)
第四步:求复数极点处的起始角 \[ \begin{aligned} \theta_{p_3}&=\pm (2k+1)\pi-\sum_{j=1,j\neq 3}^4 \angle(p_3-p_j)\\ &=\pm(2k+1)\times 180^\circ -116.6^\circ -12.5^\circ - 90^\circ\\ &=-39.1^\circ \end{aligned} \] (取\(k=0\))。则\(\theta_{p_4}=39.1^\circ\)
第五步:求实轴上分离点坐标和分离角 \[ \frac 1{\sigma_b}+\frac 1{\sigma_b+20}+\frac 1{\sigma_b+2+4j}+\frac 1{\sigma_b+2-4j}=0 \] 解得\(\sigma_b=-15.1\),分离角为\(\pm 90^\circ\)
第六步:求根轨迹和虚轴的交点。闭环特征方程为: \[ s(s+20)(s^2+4s+20)+k=0 \] 令\(s=j\omega\),代入: \[ j\omega(j\omega+20)(-\omega^2+4j\omega+20)+k=0 \] 令实部虚部都是零,有: \[ \begin{cases} \omega^4-100\omega^2+k=0\\ -24\omega^2+400\omega=0 \end{cases} \] 得\(\omega=\pm 4.1,k=1391\)。
于是,可以画出根轨迹图了。
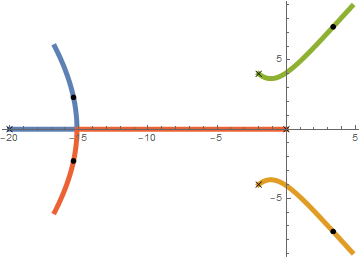
上面这张图是用
Mathematica画的,代码为:
2RootLocusPlot[k/(s*(0.05*s + 1)*(0.05*s*s + 0.2*s + 1)), {k, 0, 80},
PlotStyle -> AbsoluteThickness[5.`]]
频域分析法
系统的频率响应函数就是把\(G(s)\)里面的\(s\)换成\(j\omega\),即\(G(j\omega)\)。
在进行频域分析法时,有两件事是无论如何都要注意的:
对开环系统函数进行分析
要把系统函数各个因子的系数化为1,即: \[ G(s)=\frac{K_0(\tau_1s+1)\cdots(\tau_2s^2+2\xi_2\tau_2s+1)\cdots}{s^v(T_1s+1)\cdots(T_2s^2+2\xi_2T_2s+1)\cdots} \]
奈奎斯特图
奈奎斯特图就是在复平面上\(G(j\omega)\)的值随\(\omega\)从\(0\)变化到\(+\infty\)时的参数图像。在介绍奈奎斯特图的画法时,我将介绍两种方法。首先介绍一种公式法,然后来说明公式法的本质。
公式法
按照下面几个步骤,可以画出奈奎斯特图。
确定起点
起点按照以下公式确定: \[ G(0+)=\begin{cases} 0_+\angle(-v\frac \pi2+\angle K_0) & v<0\\[2ex] |K_0|\angle K_0 & v=0\\[2ex] \infty\angle(-v\frac \pi2+\angle K_0) & v>0 \end{cases} \] 其中\(v\)是传递函数分母里面单个\(s\)的指数,\(K_0\)是分子上提出来的系数。
然后,看(分母中\(s\)一次项的系数之和-分子中\(s\)一次项的系数之和),如果这个值大于零,那么就在前进方向的坐标轴的左侧,否则在右侧。
以 \[ G(s)=\frac 1{s(s+1)(2s+1)} \] 为例,有\(v=1>0\),所以\(G(0+)=\infty\angle (-\frac \pi2+0)=\infty\angle -90^\circ\)
分母中\(s\)的系数之和为\(1+1+2=3\),分子中\(s\)的系数之和为零,所以在前进方向坐标轴的左侧,即正向纵轴的左侧,即从第四象限起笔
确定终点
终点按以下公式确定: \[ G(j\infty)=\begin{cases} |K^*|\angle\left[-(n'+m')\frac \pi2+\angle K_0\right] & n=m\\[2ex] 0_+\angle\left[-(n'+m')\frac \pi2+\angle K_0\right] &n>m \end{cases} \] 其中\(m\)是分子的总次数,\(n\)是分母的总次数,\(m'=m_a-m_b\),\(n'=n_a-n_b\)
\(*_a\)代表分子/分母中最小相位环节(就是\(s\)前面系数是正的)的总阶数,\(*_b\)代表分子/分母中非最小相位环节的总阶数。
继续以上面的系统为例,分子中次数为零,最小相位环节阶数为零;分母中次数为3,最小相位环节总阶数也是3,所以 \[ G(j\infty)=0_+\angle\left[-(3-0)\frac \pi2+0\right]=0_+\angle -270^\circ \] 于是,知道了起点和终点,我们就可以初步画出\(0_+\to\infty\)的图像了:
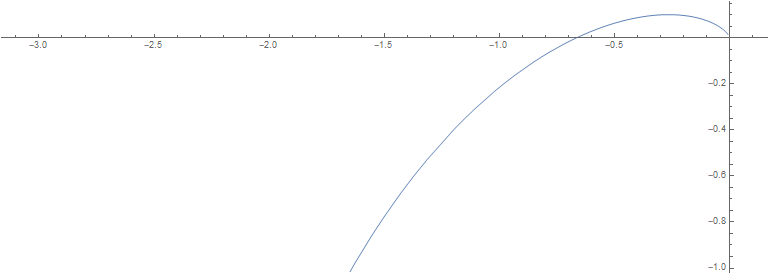
绘图代码:
1
2ParametricPlot[{Re[(1)/(I*w*(I*w + 1)*(2*I*w + 1))],
Im[(1)/(I*w*(I*w + 1)*(2*I*w + 1))]}, {w, 0.01, 3}]补充虚圆
为什么说上面的是初步呢?因为还有\(0\to0_+\)这部分的没有画,而且这部分还很重要。
如果\(v=0\),那么不用画。
如果\(G(s)\)在原点上有重根,即\(v>0\),那么以\(\angle K_0\)为开始,半径无穷大,顺时针转\(+v\frac \pi2\),接到上面那个图像的起点处。
*如果\(G(s)\)在虚轴上有\(n\)重共轭极点\(\pm j\omega_n\),则: \[ G(s)=\frac 1{(s^2+\omega_n^2)^u}G_2(s) \] 其中\(G_2(s)\)是没有\(n\)重共轭极点的。那么从\(G_2(j\omega_n)\)开始,以半径为无穷大,顺时针转\(+u\pi\),接到起点处。
还是对于上面这个例子,属于第二种情况,于是可以画出:
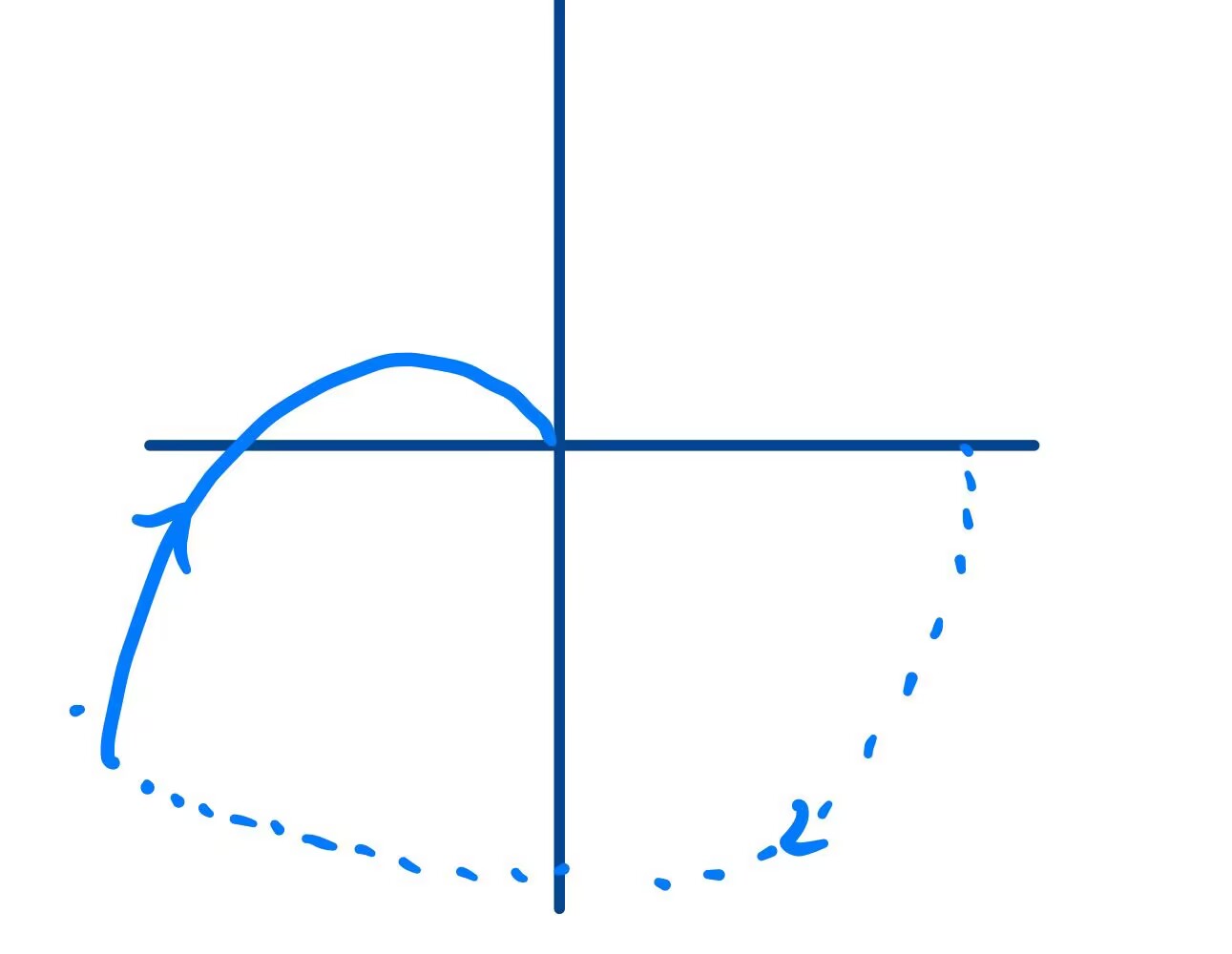
定义法
确定起点
说起起点,就是计算 \[ \lim_{\omega\to 0+}G(j\omega) \] 不就行了吗?先来看模长部分,那当然是\(v>0\)就是无穷大,因为分母是零;\(v<0\)是零,因为分子是零,这是显然的。然后看相位,众所周知复数相乘就是相位相加,复数相除就是相位相减,所以相位就是分子的相位减去分母的相位之和了。考虑一个\((\tau j\omega+1)\),当\(\omega\to 0_+\)时,这玩意就趋向于\(1\),对应的相位就是\(0\),所以不用管,只看\(j\omega\)单独的那一项,一个它的相位是\(90^\circ\),总共有\(v\)个它,这就是公式法里面的 \[ -v\frac \pi2+\angle K_0 \] 的来历。
确定终点
终点就是 \[ \lim_{\omega\to \infty}G(j\omega) \] 幅值分析略,看相位。最小相位系统就是\((j\omega+1)\),非最小相位系统就是\((-j\omega+1)\),当\(\omega\to \infty\)的时候他俩分别就是\(j,-j\),对应的相位就是\(90^\circ,-90^\circ\)。这就是公式法里面的 \[ -(n'+m')\frac \pi2+\angle K_0 \]
画出虚圆
这里只说第二种情况。如果\(\omega=0\)了,那么值显然是\(sgn[K_0]\infty\),实数,所以要从\(\angle K_0\)开始。但是从\(0+\)开始那它就不是实数,就有一个“确定起点”的那个角度,这时候虚圆就是把这俩连起来就行。
画图完成以后,还要计算一个点,那就是图像和横轴的交点,名叫穿越点,对应的频率叫穿越频率。
奈奎斯特稳定判据
利用奈奎斯特图判断闭环系统的稳定性,需要计算 \[ Z=P-2N \] 如果\(Z=0\),那么稳定。
其中,\(P\)是开环中实部大于零的极点的个数,也可以对分母用劳斯表,看第一列的符号改变次数。
\(N\)是曲线穿越\((-\infty,-1)\)这段横轴的总次数,但是有正有负:
- 虚圆穿越,总是负的
- 实线穿越,以\((-1,0)\)作为视点,看它是顺时针(负)还是逆时针(正)
- 如果起始点、终止点在轴上,算\(0.5\)次
波特图
波特图由两张半对数坐标图组成,其中一张表征幅频特征,一张表征相频特征。其横坐标是频率,为对数坐标;幅频纵坐标是dB,相频纵坐标是线性。绘制波特图首先要记住两个原则
- 如果两个传递函数互为倒数,那么波特图关于横轴镜像对称
- 如果两个传递函数互为共轭(即\(s\)换成\(-s\)),那么幅频曲线相同,相频关于横轴镜像对称
然后记住两个典型环节:
惯性环节 \[ \frac 1{\frac{s}{\omega_n}+1} \] 对应的幅频斜率为\(-20\)dB/十倍频,对应的相频变化量为\(-90^\circ\)
震荡环节 \[ \frac 1{\left(\frac s {\omega_n}\right)^2+2\xi\frac s{\omega_n}+1} \] 对应的幅频斜率为\(-40\)dB/十倍频,对应的相频变化量为\(-180^\circ\)
然后可以开始画了。画的步骤如下。在下面的例子中,传递函数为: \[ G(s)=\frac{100(1+\sqrt{10}s)}{(-100s^2+20s+1)(-0.001s^2+\frac{\sqrt{10}}{3000}s+1)} \]
把系统函数按转折频率从低到高排列,并把因子写成上面的那种形式,然后在横轴上标出转折频率 \[ G(s)=100\cdot \frac{1}{\left(\frac{s}{0.1}\right)^2+2\frac{s}{0.1}+1}\cdot \left(\frac{s}{\frac{1}{\sqrt{10}}}+1\right)\cdot \frac{1}{\frac{s}{10\sqrt {10}}^2+\frac 1{30}\frac{s}{10\sqrt {10}}+1} \] 所以转折频率为\(0.1,1/\sqrt {10},10\sqrt{10}\)
低频段(即比最低的转折频率还低的一段):幅频斜率为\(-20v\)dB/十倍频,相位起点为\(-v\cdot 90^\circ+\angle K_0\),然后根据幅频曲线一定经过\((|K_0|^{1/v},0)\)或者\((1,20\lg|K_0|)\)来确定幅频曲线的位置
在本例中,\(v=0,\angle K_0=0\),\(-20v=0\),\(20\lg K_0=40\)
幅频图中,每段以转折频率为界限,调整斜率,在原有斜率的基础上增加目前环节对应的斜率。
相频图中,每个转折频率代表相频图在\(0.1\omega_c,10\omega_c\)上变化了\(\Delta \varphi\),不同的转折频率之间相互叠加
(可选)在二阶环节对应的转折频率处补充一个高度为\(20\lg |1/2\xi|\)的尖峰
计算幅频曲线和\(\omega\)轴的交点
对数判据
要用波特图判断闭环系统的稳定性,同样要计算 \[ P-2N \] 其中\(P\)是开环中实部大于零的极点的个数,\(N\)是在\(L(\omega)>0\)即幅频图为正值的部分中,相频曲线穿过\((2k+1)\pi\)的次数之和,向上穿越算正数,向下穿越算负数
稳定裕度
稳定裕度是衡量系统相对稳定性质的量,分为相位裕度和增益裕度。
相位裕度的定义是在幅频波特图和横轴的交点\(\omega_c\)处,使系统达到临界稳定状态的附加相移,有: \[ \gamma=180^\circ+\angle G(j\omega_c)H(\omega_c) \] 在奈奎斯特图中,相位裕度\(\gamma\)指的是曲线和单位圆的交点和原点的连线与负实轴之间的夹角。
增益裕度\(K_g\)的定义是在相频波特图和\(-180^\circ\)的交点\(\omega_g\)处,使得系统达到临界稳定状态所需增大的增益倍数,一般用dB表示,有: \[ K_g=-20\lg|G(j\omega_g)H(j\omega_g)| \] 在奈奎斯特图中,增益裕度是曲线和负实轴的交点离原点的距离的倒数。
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
