自动控制原理笔记(时域分析)
控制系统基础知识
在本节,将对自动控制原理中的一些基础概念给出定义,以方便后续的讨论。
控制系统的性能要求
自动控制系统的目标是使得被控量按照指定规律变化。系统受到外加信号作用之后,被控量随着时间变化并趋于一定规律的全过程被称为系统的动态特性。
系统的稳定性指的是系统进入稳态或者恢复工作状态的能力,即瞬态响应是否会随着时间的延续而趋向于0。系统的平稳性指的是当系统稳定时,要求\(c(t)\)即输出信号的振荡小,在时域分析中通常用超调量\(M_p\)表示。系统的“快速”指的是动态过程(即瞬态响应)持续的时间长短。系统的准确度指的是过渡到新的平衡状态后最终保持的精度。
控制系统的数学模型
控制系统通常用微分(差分)方程、方框图等形式表示。一个一般的闭环系统的方框图为:
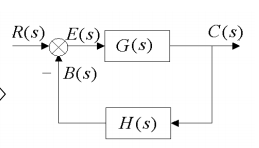
其中\(G(s)\)称为前向传递函数,\(G(s)H(s)\)称为开环传递函数,当\(H(s)=1\)时,开环传递函数和前向传递函数相等。而 \[ T(s)=\frac {C(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)} \] 称为闭环传递函数,它也是整个闭环系统的传递函数。
对于一般的控制系统,其控制元件的数学模型都是由几种简单的因子或者典型单元结构组成的,常称为“典型环节”。常见的典型环节有:
放大环节
微分方程为 \[ y(t)=Kx(t) \] 传递函数为 \[ G(s)=K \]
惯性环节
微分方程为 \[ T\frac{dy(t)}{dt}+y(t)=x(t) \] 传递函数为 \[ G(s)=\frac{1}{Ts+1} \] 其中\(T\)叫做时间常数,典型的惯性环节是RC网络。
一阶微分环节
微分方程为 \[ y(t)=\tau \frac {dx(t)}{dt}+x(t) \] 传递函数为 \[ G(s)=\tau s +1 \]
积分环节
微分方程为 \[ \frac{dy(t)}{dt}=x(t) \] 传递函数为 \[ G(s)=\frac 1s \]
理想微分环节
微分方程为 \[ y(t)=\frac{dx(t)}{dt} \] 传递函数为 \[ G(s)=s \]
此外,还有震荡环节、二阶微分环节等。
时域分析法
在时域分析法中,往往选择典型的初始状态(零状态,即\(t=0-\)时,\(c(t)\)的任意阶导数为零),典型的输入信号(如阶跃、斜坡、加速度、冲击、正弦信号),求出典型的时间响应,然后考察系统的性能。
一阶系统时域分析
一个典型的闭环一阶系统的框图如下:
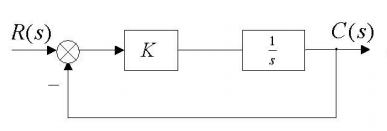
其闭环传递函数为 \[ T(s)=\frac{1}{\frac 1Ks+1}=\frac{1}{Ts+1} \] 在\(-K=-1/T\)处有一个极点。
其单位阶跃响应为: \[ c(t)=\left(1-e^{-\frac 1T t}\right)u(t) \] 其时域性能只由一个参数决定,即\(-1/T\),其中\(T\)也叫时间常数,它表示系统响应达到稳态值的\(63.2\%\)所需的时间。时间常数越小,系统的速度越快。其调整时间一般取\(t_s=3T(5\%\Delta)\)或\(t_s=4T(2\%\Delta)\),稳态误差为零。
其单位斜坡响应为 \[ c(t)=(t-T)+Te^{-t/T} \] 所以具有稳态误差,为\(T\)。
二阶系统时域分析
一个典型的二阶系统如下:
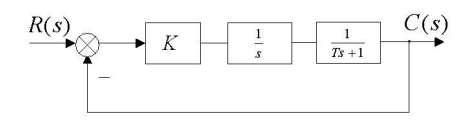
其闭环传递函数为 \[ T(s)=\frac{K}{Ts^2+s+K} \] “标准形式”为: \[ T(s)=\frac{\omega_n^2}{s^2+2 \xi \omega_n s+\omega_n^2}=\frac{\omega_n^2}{\left(s-s_1\right)\left(s-s_2\right)} \] 之所以要写成看起来这么复杂的样子,是因为其中的参数\(\xi,\omega_n\)等有其物理意义。其中\(\omega_n=\sqrt{K/T}\)叫做“无阻尼振荡频率”,\(\xi =1/(2\sqrt{KT})\)叫做“阻尼比”。阻尼比决定了系统阶跃响应的模式。
欠阻尼系统(\(\xi \in (0,1)\))
两个极点\(s_1,s_2\)互为共轭复根。阻尼自然频率\(\omega_d=\omega_n\sqrt{1-\xi^2}\)。欠阻尼系统的阶跃响应时域波形大概是这个样子:
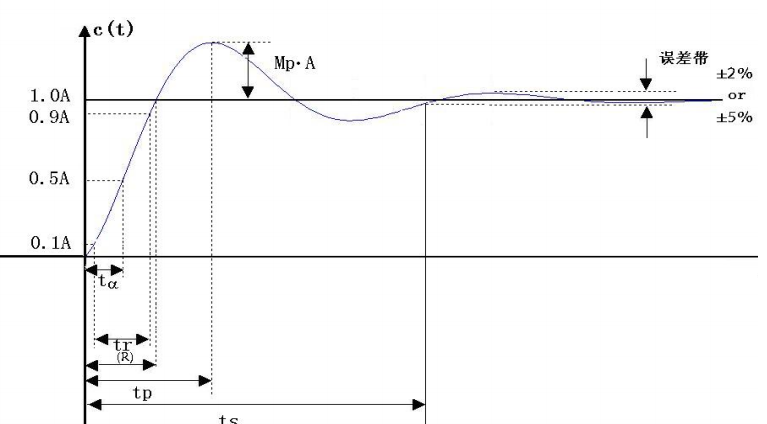
可以看到里面有很多参数。下面介绍几个比较重要的
上升时间\(t_r\)
指的是从稳态值的\(10\%\)上升到\(90\%\)所需的时间。有: \[ t_r=\frac{\pi-\beta}{\omega_d} \]
峰值时间\(t_p\)
指的是系统达到最大值所需的时间。有: \[ t_p=\frac \pi {\omega_d} \]
最大超调量\(M_p\)
指的是响应峰值和稳态值之间的归一化差值。有: \[ M_p=\frac{c(t_p)-c(\infty)}{c(\infty)}=e^{-\frac{\pi \xi}{\sqrt{1-\xi^2}}} \]
调节时间\(t_s\)
调节时间指的是满足: \[ \forall t>t_s,|c(t)-c(\infty)|\leq \Delta c(\infty) \] 的最小\(t_s\)。有: \[ t_s= \begin{cases}\frac{4}{\xi \omega_n} & 2 \% \Delta \\ \frac{3}{\xi \omega_n} & 5 \% \Delta\end{cases} \]
过阻尼系统(\(\xi >1\))和临界阻尼系统(\(\xi=1\))
这两种情况下,\(c(t)\)是单调上升过程,系统近似为一阶系统,单位阶跃响应近似表示为: \[ c(t)=1-\exp [-(\xi -\sqrt{\xi ^2-1})\omega_n t] \]
稳定性分析
\(H(s)\)的极点如果全部位于左半平面,则系统稳定。当虚轴存在一阶零点时,称为边界稳定或者震荡稳定;当右半平面有极点,或者虚轴上有高阶极点时,称系统不稳定。
首先基于\(H(s)=N/D\)的阶次进行分析。其中\(N\)是\(m\)阶多项式,\(D\)是\(n\)阶多项式。
如果\(m>n\),系统一定存在一个无穷远点处的极点。基于这个事实,有以下系统稳定的必要条件:
- \(m\leq n\)是系统稳定的必要条件
- \(m>n+1\)时,系统一定不稳定
基于分母多项式(也叫特征多项式)的根的分布判别
必要条件
- \(D(s)\)的所有系数都同号
- \(D(s)\)不缺项,或者缺全部的奇次或偶次项
上面两个条件是必要条件,只要任一条件不被满足,系统就不是稳定的。但是即使全部满足,系统也不一定稳定。例如: \[ D(s)=2s^3+s^2+3s+9 \]
劳斯判据
劳斯判据就是列劳斯表,然后看第一列是不是全同号。劳斯表是这样列的:
前两行,第一行从前往后是\(a_n,a_{n-2},a_{n-4},\cdots\),直到下标小于\(0\);第二行,是\(a_{n-1},a_{n-3},\cdots\),直到下标小于\(0\)。设劳斯表第\(i\)行第\(j\)列的元素是\(m_{ij}\),在第三行之后,有: \[ m_{ij}=-\frac{1} {m_{i-1,1} }\begin{vmatrix} m_{i-2,1} & m_{i-2,j+1}\\ m_{i-1,1} & m_{i-1,j+1}\\ \end{vmatrix} \] 单看这些下标可能还比较抽象。实际上就是说,第三行以后的劳斯表的元素都是一个二阶行列式的相反数除以它上一行的第一个数。这个二阶行列式的左侧一列是它上一行和上上一行的第一个数,右侧一列从上一行和上上一行的第二个数开始,随着当前要算的这个元素在自己的行中向右移动而向右移动。
在计算过程中,可能会出现两种特殊情况。
其一是某一行的第一个数是零,但其余各项不全为零。这时候只需要把它用一个很小的正数\(\epsilon\)代替然后继续算就行。
其二是某一行的所有数都是零,这代表着系统可能存在互为相反数的实根,或者共轭虚根,或者关于原点对称的共轭复根。这时可以把全零行的上一行的系数构造一个辅助多项式(最高次是行号,然后每个系数降2次),对其求导,并把求导结果带入全零行,然后继续算。需要注意:辅助多项式的根也是原方程的根。
稳态误差分析
如果输入信号\(r(t)\)和输出信号\(c(t)\)是同量纲、同数量级的,那么系统误差定义为: \[ e(t)=r(t)-c(t) \] 但是实际上这并不可能,因为很多系统都是用电压输入,而输出的被控量很可能是温度,速度等物理量。这就需要用一个传感器把被控量转换为和输入量同量纲同数量级的量,并放在反馈支路。此时系统误差定义为: \[ e(t)=r(t)-b(t) \] 为计算稳态误差,考虑终值定理(使用条件:\(E(s)\)极点都在\(s\)左半平面),有: \[ \lim _{t\to \infty}e(t)=e_s=\lim_{s\to 0}sE(s)=\lim _{s \rightarrow 0} s \cdot \frac{R(s)}{1+G(s) H(s)} \] 注意到,系统稳态误差和输入信号以及开环传递函数\(G(s)H(s)\)有关。稳态误差仅对稳定系统才有意义。
系统开环传递函数一般为: \[ G(s) H(s)=\frac{K\left(\tau_1 s+1\right) \cdots\left(\tau_2^2 s^2+2 \xi \tau_2 s+1\right) \cdots}{s^N\left(T_1 s+1\right) \cdots\left(T_2^2 s^2+2 \xi T_2 s+1\right) \cdots} \] 注意:这里的系数\(K\)的提出是为了把后面的每一项的常数项都设置为\(1\),称为系统的开环放大倍数。分母里的\(s^N\)的指数\(N\)表示系统开环串联的积分环节的个数,决定了系统的型别,即“\(N\)型系统”
接下来就输入信号和系统型别来讨论稳态误差:
输入\(R(s)=1/s\)
此时有: \[ e_{ss}=\lim _{\mathrm{s} \rightarrow 0} \frac{1}{1+G(s) H(s)}=\frac{1}{1+\lim _{\mathrm{s} \rightarrow 0} G(s) H(s)}=\frac{1}{1+K_p} \] 其中\(K_p=\lim _{s\to 0}G(s)H(s)\)称为阶跃误差系数,也叫静态位置误差系数。
- 0型系统:\(K_p=K,e_{ss}=1/(1+K)\)
- \(0\)型以上系统:\(K_p=\infty,e_{ss}=0\)
输入\(R(s)=1/s^2\)
此时有: \[ e_{s r}=\lim _{s \rightarrow 0} \frac{1}{s+s G(s) H(s)}=\frac{1}{\lim _{s \rightarrow 0} s G(s) H(s)}=\frac{1}{K_v} \] \(K_v\)叫做斜坡误差系数,也叫静态速度误差系数。
| 系统型别 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(K_v\) | \(0\) | \(K\) | \(\infty\) | \(\infty\) |
| \(e_{sr}\) | \(\infty\) | \(1/K\) | \(0\) | \(0\) |
输入\(R(s)=1/s^3\)
此时有: \[ e_{s p}=\lim _{s \rightarrow 0} \frac{1}{s^2+s^2 G(s) H(s)}=\frac{1}{\lim _{s \rightarrow 0} s^2 G(s) H(s)}=\frac{1}{K_a} \] \(K_a\)叫做抛物线误差系数,也叫静态加速度误差系数。
| 系统型别 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| \(K_a\) | \(0\) | \(0\) | \(K\) | \(\infty\) |
| \(e_{sp}\) | \(\infty\) | \(\infty\) | \(1/K\) | \(0\) |
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
