信息的统计度量
信息量
自信息量
从信源中获取信息的过程就是其不确定性缩减的过程,在统计分析中,使用概率作为衡量不确定性的一种度量。因此,信息量和概率是紧密相关的。任意事件的自信息量的定义为该事件发生的概率的对数的负值,即:
在总体中,事件发生的信息量为: 可见:小概率事件包含的不确定性大,所以它带来的信息量也大。
信息量所用的单位随着对数的底变化而变化,常用的有:
| 2 |
比特(bit) |
| e |
奈特(nat) |
| 10 |
哈特(hat) |
需要说明的是,信息量本身是纯数,没有量纲。这里的“单位”只是为了表示不同底的对数值。
二维联合总体上的元素的信息量为: 在二维联合总体中,事件在事件给定的条件下的条件自信息量为:
互信息量
对于一个信息传输系统来说,如果信道中没有干扰,那么信源发出信号以后,信宿一定可以准确地收到消息,此时获得的信息量就是的不确定度,即信源发出的所含有的全部信息。但是实际上信道不可能没有干扰,这时候通过信道会产生污染,信宿收到的消息将不同于,只能通过条件概率推测信源发出的概率。
对于两个离散随机总体,事件的出现给出关于事件的信息量定义为互信息量,为: 意思是,互信息量是一种不确定性的度量,等于先验的不确定性减去尚存在的不确定性。
互信息量有以下性质:
互易性:
可以为0:当相互独立时,互信息量为零
可正可负:正值意味着事件的出现有助于肯定事件的出现,反之则是不利。
任何两个事件之间的互信息量不大于其中任意一个事件的自信息量
在联合总体中,给定的条件下,和的互信息量叫做条件互信息量,即: 在上述联合总体上,还有和之间的互信息量,有: 意思是:同时出现提供的有关的信息量等于提供的信息量和给定的条件下,提供的信息量之和。
离散集(总体)的平均自信息量
之前讨论的自信息量都是对于一个事件来说的。为了讨论整个总体,需要定义平均自信息量: 平均自信息量也叫做总体的信息熵。因为信息熵仅仅是总体的概率分布的函数,所以又可以记作: 其中,所以它实际上是一个元函数。
在联合集上,条件自信息量的概率的加权平均值定义为条件熵,即: 对于条件熵,有: 在联合集上,每对元素的自信息量的概率加权平均值定义为联合熵,即: 对于联合熵,有: 当X和Y统计独立时,取得等号。
熵函数有以下特征:
对称性:指无论如何改变概率矢量中的元素排列顺序,保持不变
非负性:,当且仅当中有且只有一个,其它全是
扩展性: 意思是:一个事件的概率同总体中其它事件相比极小时,它对于总体熵的贡献可以忽略不计。
可加性:
极值性
上凸性:是的严格上凸函数,即:
对于两个概率矢量,有:
离散集的平均互信息量
在联合集上,由提供的关于集的平均条件互信息量是由提供的关于元素的互信息量的加权平均,即: 平均条件互信息量在上的加权平均是两个总体的平均互信息量,即: 平均互信息量非负、互易,而且和通信熵具有如下的关系:
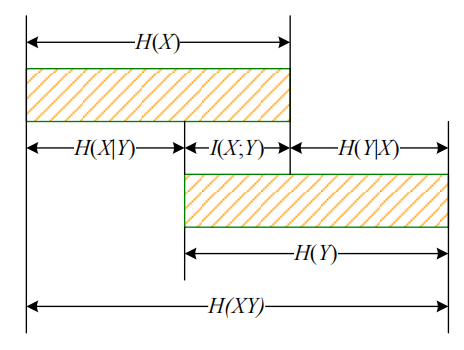 image-20230415213620301
image-20230415213620301
离散信源
离散无记忆信源
离散无记忆信源可以用下面的概率分布描述: 其次扩展信源是具有个符号的离散无记忆信源,为: 次扩展信源的熵为原信源的倍,即:
离散平稳信源
如果一个信源产生的随机序列满足:
所有都取值于有限的信源符号集合
对所有的非负整数,对所有的,有:
也就是说,这个信源发出的符号序列的概率分布和时间起点无关,那么这个信源称为离散平稳信源。
如果有 即任意时刻信源发出单个符号的概率相同,那么叫做“一维平稳信源”;如果随机序列的二维联合分布也和时间起点无关,称为二维平稳信源。如果对任意正整数,其联合分布都和时间起点无关,称为完全平稳信源,简称为平稳信源。
对二维平稳信源来说,有联合熵:
条件熵:
因为
所以 $$
$$ 即:联合熵=前一个符号的信息熵+前一个符号已知时信源发出下一个符号的条件熵。
对于平稳有记忆N次扩展信源,有平均符号熵: 当信源符号序列长度趋于无穷时,有极限熵: N次扩展信源熵的性质有:
- 条件熵随增加非递增
- 平均符号熵随增加非递增
- 极限熵存在,且
马尔可夫信源
如果系统在时刻处于状态,那么将来时刻的状态和过去的都无关,只和现在时刻的状态有关,这样的特性叫做马尔可夫特性,这样的系统叫做马尔可夫链(有限状态一阶马尔可夫链),用数学语言描述,就是: 引入转移概率: 意思是已知时刻系统处于状态,经过步后系统转移到状态的概率。在有限状态一阶马尔可夫链中,我们主要关注,简记为,即: 类似地,定义步转移概率为。
因为系统在任意时刻都可能处于任意状态,所以一般用状态转移矩阵来描述,时刻的步转移矩阵定义为: 如果在马尔科夫链中,,即转移概率和无关,那么称之为齐次马尔可夫链,也叫遍历的马尔可夫链。齐次马尔科夫链的转移矩阵可以表示为: 且有C-K方程: 若齐次马尔可夫链对一切存在不依赖于的极限: 且满足:
那么称其有平稳性,称为平稳分布,其中是马尔科夫链的初始分布。意思是,无论系统从哪个状态出发,当转移的步数足够多时,转移到特定状态的概率都近似等于一个常数。稳态分布存在的充要条件是:存在一个正整数,使得中的所有元素都大于零。
如果稳态分布存在,那么可以设稳态分布矢量,其中表示稳态分布中的,通过解方程 可以求解稳态分布,且稳态分布具有唯一性。
具有阶马尔可夫特性(即下一个时刻输出的符号仅和前个符号有关,和更前的符号无关)的信源称为阶马尔可夫信源。遍历的阶马尔可夫信源的极限熵为其阶条件熵,即:
相关性和冗余度
信源输出符号间的依赖关系越强,信源熵就会减小。这就是信源的相关性。当信源输出符号间的相关程度越长,信源的实际熵越小,趋于极限熵;当信源输出符号之间不存在相互依存关系且为等概分布,信源实际熵趋于最大熵,其中是信源输出符号集的符号数目。定义信源剩余度:
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:


