数字电路·模拟之章
为什么叫模拟之章呢?是因为这篇主要是涉及模拟电路的部分。
门电路
CMOS门电路
要研究CMOS门电路,首先要认识MOS器件以及它们的特性。
MOS管的基本概念
MOS管全名叫“结型场效应晶体管”,我们平常见到的有以下四种

注意看:箭头方向决定是N还是P,线的虚实决定是增强还是耗尽。
MOS管的符号也有简化画法,如下:
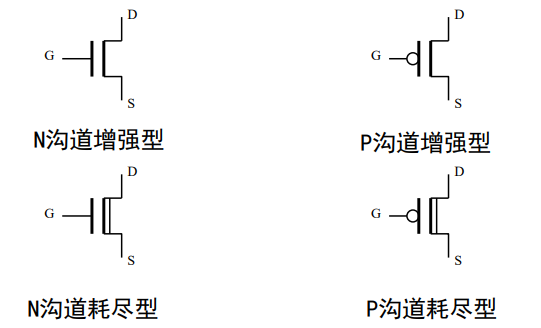
它们的特性按P、N和增强、耗尽,有所不同:
- N沟道的,当
- 增强型,开启电压为正。以
为了加深对这个特性的理解,我们来分析一下下面这个电路:
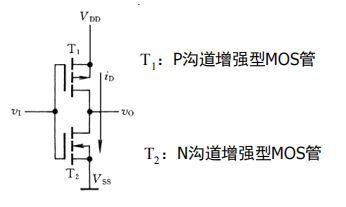
约定:
- 当
- 当
- 综上所述,这是个非门。
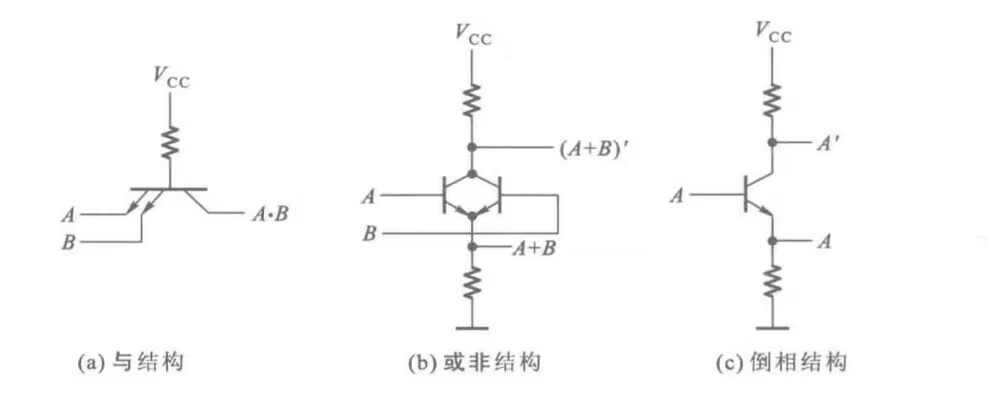
经典门电路的MOS管实现
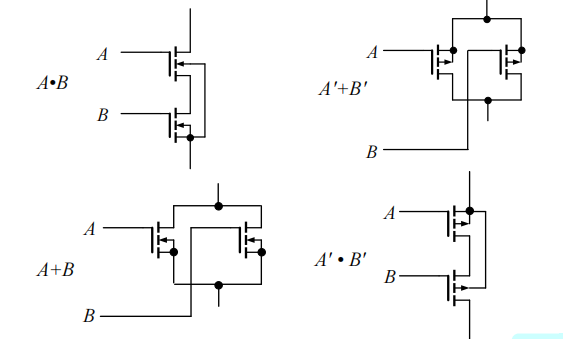
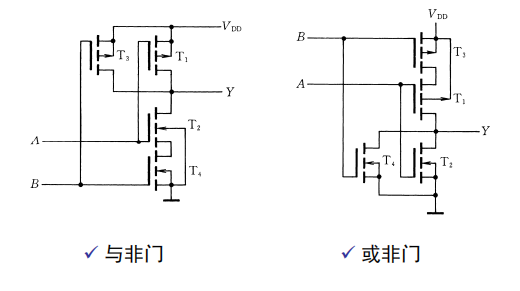
对于CMOS器件构成的门电路,不允许输入端悬空,输入端经电阻接地时和低电平等效,输入端经电阻接电源时和高电平等效。
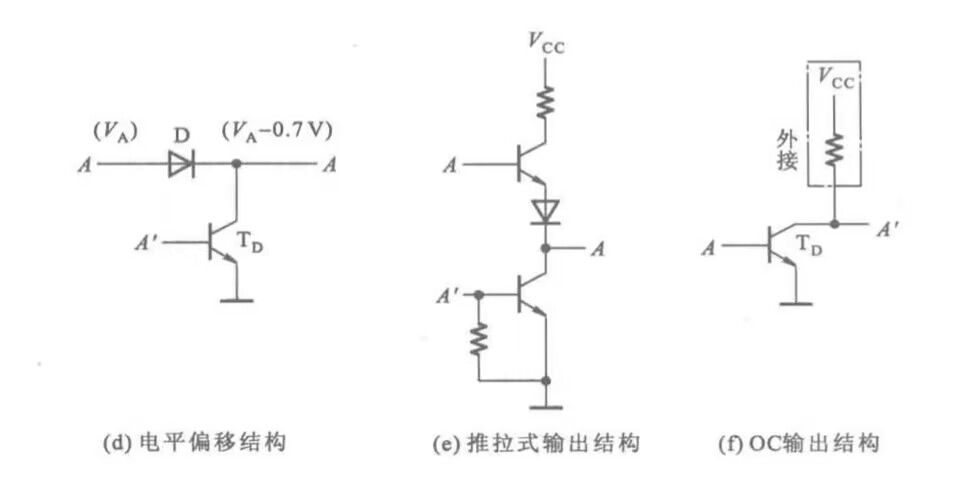
OD门
OD门全称为漏极开关输出门电路,它的电路长这样:
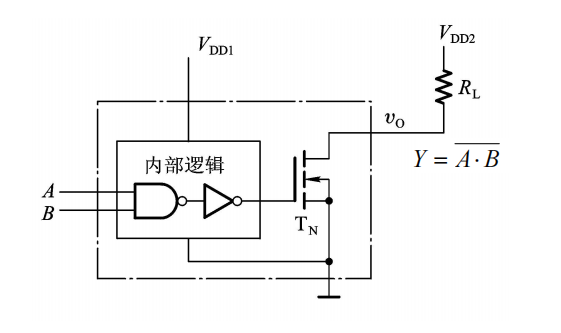
其逻辑符号为门电路符号里面加一个带下划线的菱形,如下:
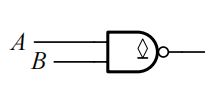
OD门要正常工作,必须把输出端经过一个上拉电阻和电源相连。也就是电路详图中的
把多个OD门的输出端直接接在一起,可以构成“线与”逻辑,如下图所示:
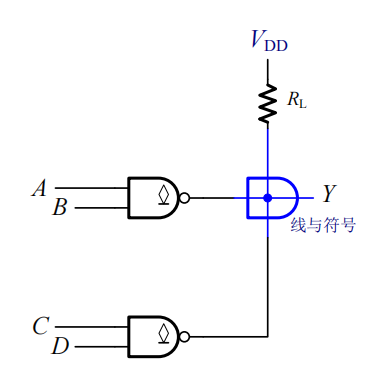
这时,有
在选取
传输门
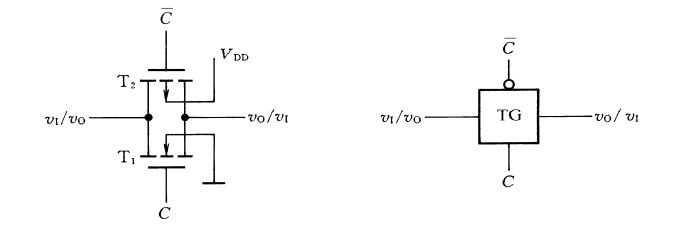
其特性为:
三态门
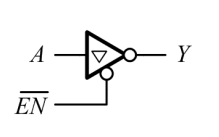
三态门是一个正常的门电路外加一个
TTL门电路
我也不会分析,所以分析略。
这里这个OC门(集电极开路输出的门电路)就和前面那个OD门意思差不多,也有线与,也得算
对于TTL门电路,输入端悬空等效于逻辑高电平;输入端经过几十千欧以内的电阻接电源,等效于逻辑高电平;输入端经过几十欧的小电阻接地等效于低电平,当电阻升高到一定程度(一般是几千欧)以后,等效为高电平。
脉冲波形的产生和整形电路
施密特触发器
施密特触发器是脉冲波形变换中的常用电路。它具有以下两个特点:
- 输入信号本来是低电平,上升的过程中电路状态发生转换时对应的输入电平,和输入信号本来是高电平,下降的过程中电路状态发生转换时对应的输入电平不相等
- 在电路状态变化的过程中,电路内存在正反馈过程,从而使得电压波形非常陡峭
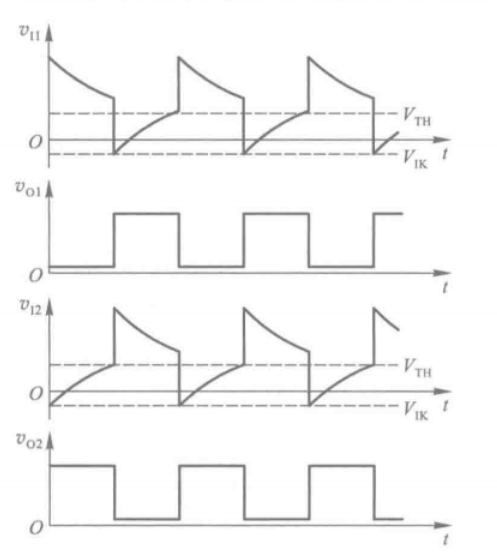
施密特触发器的电路图如下:
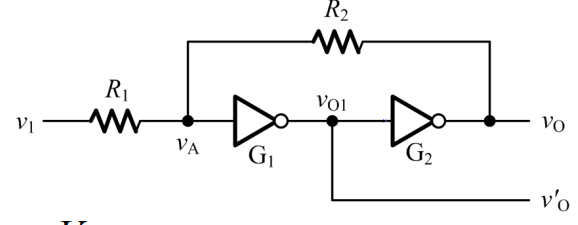
当
在上述过程中,状态转换发生的瞬间,此时
同理,当
同样,有:
于是,可以得到施密特触发器的电压传输特性:
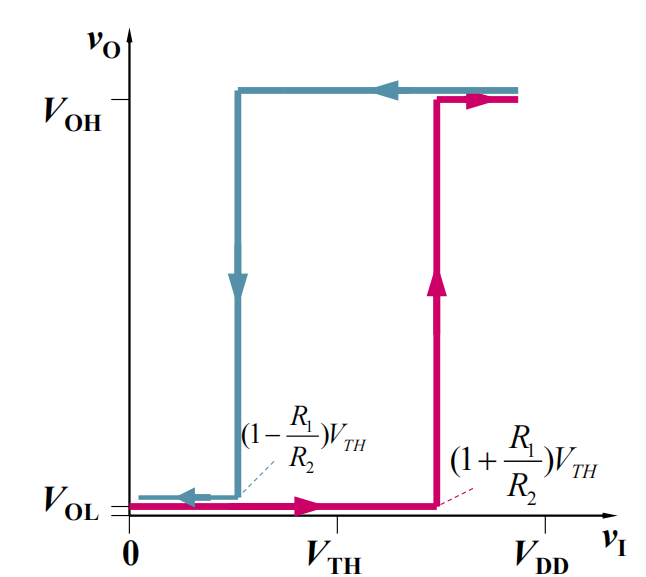
中间的部分叫做回差电压:
施密特触发器的电路符号如下:
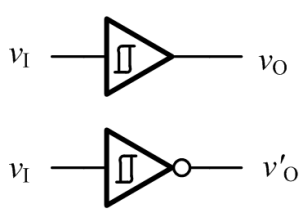
上面的同相输出,下面的是反相输出。
单稳态电路
单稳态电路具有以下特点:
- 具有稳态、暂稳态两个不同的工作状态
- 在外界脉冲的触发下,从稳态进入暂稳态,并在暂稳态停留一段时间后恢复稳态。这段时间的长度只和电路本身的参数有关,和触发脉冲的持续时间,强度无关。
这个工作特性可以类比声控灯,触发脉冲就是声音,无论你拍个手,还是长时间地播放声音,无论声音多大,只要能触发,它一次就亮那么长时间。
微分型单稳态电路
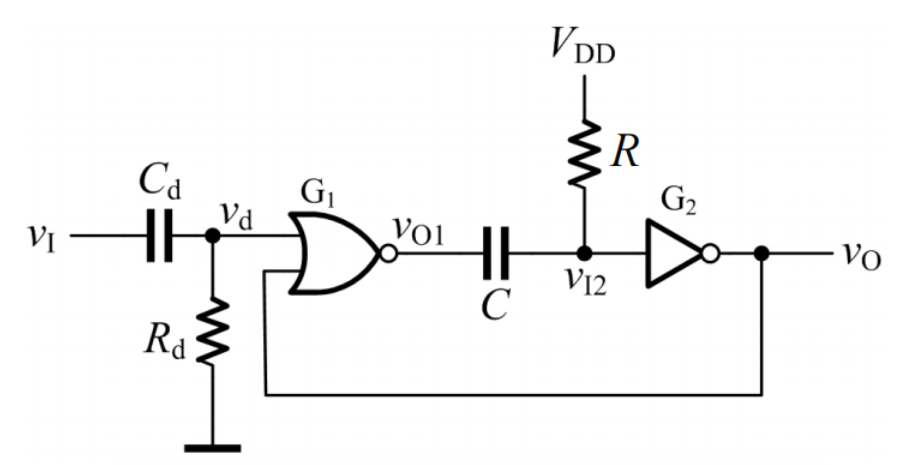
如图,微分型单稳态电路由一些电阻、电容、或非门和非门构成。其前级由
输入端本来是低电平,当向输入端
当
这时,
全过程的电压波形如下:
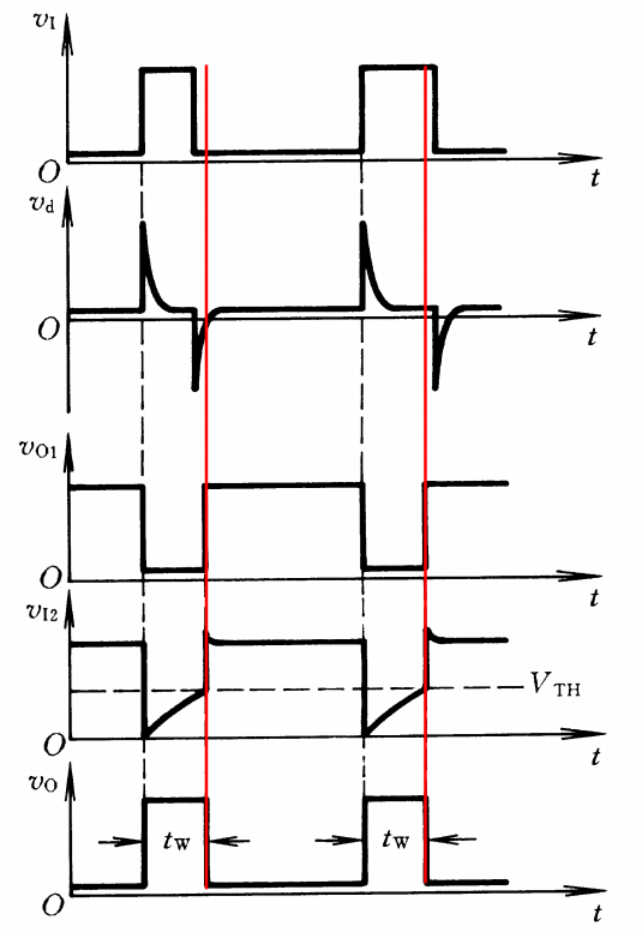
我们考察
当
积分型
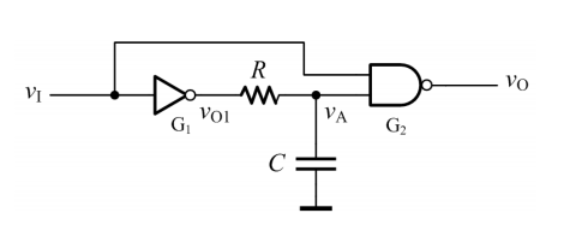
如图是用与非门、非门、积分电路构成的积分型单稳态电路。
当输入正脉冲时,
此时,电容开始放电。随着电容的放电,
全过程电压波形图如下:
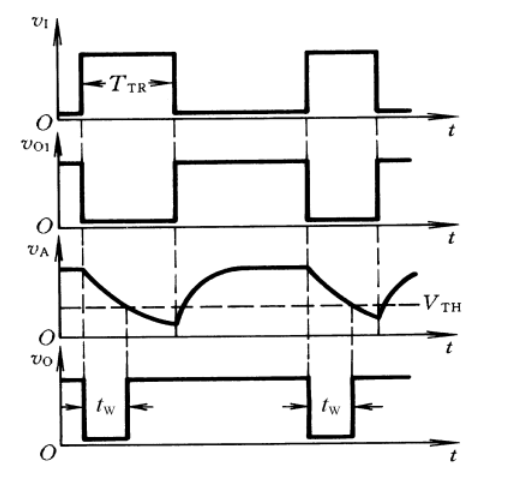
在计算电容放电过程时,有放电等效电路:
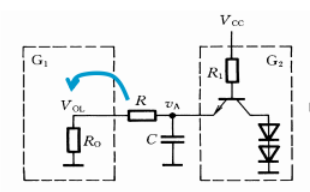
放电时,相当于
多谐振荡器
对称式多谐振荡器
对称式多谐振荡器的电路图如下:
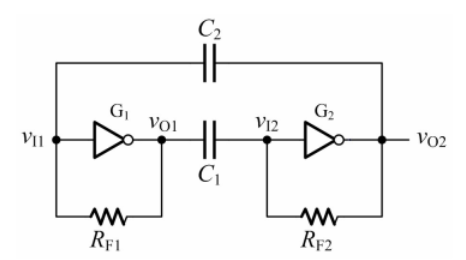
那么有人就说了:这也不对称啊?其实,它可以画成这样的形式:
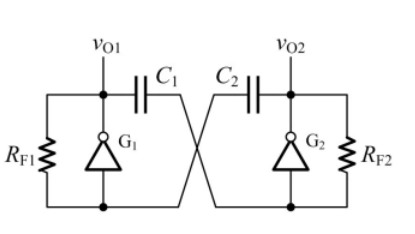
对称式多谐振荡器是没有“稳态”的,
现在,因为某些原因,给
需要注意的一点是,在接下来的分析里,我们要明确哪些电压是有外界电源保持的,哪些电压是纯数字(只有两个状态的),哪些电压是没有外界电源保持的,哪些电压是模拟(可以连续变化的)。因为这样才能知道是谁在对谁充电、画波形图时也比较方便。
有外界电源保持的电压,是纯数字的,作为门的输出端口电压出现;没有外界电源保持的电压,是模拟的,作为门的输入端口的形式出现。
对于
对于
电路的充放电回路示意图如下:
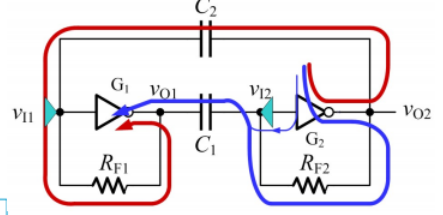
接下来,我们详细分析一下充放电过程。
对于
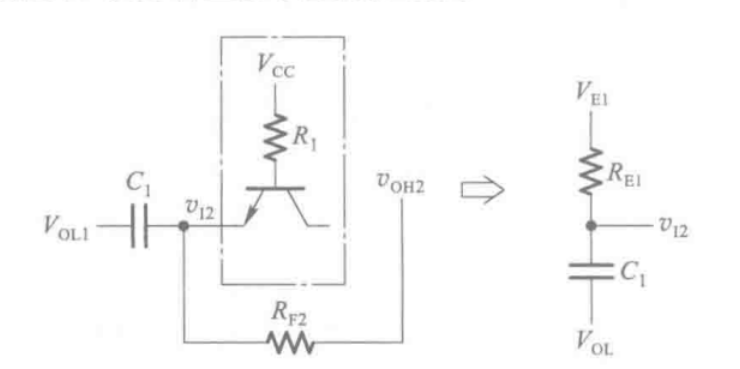
由戴维南定理,首先把所有电源接地,看进去等效于两个电阻并联,于是有:
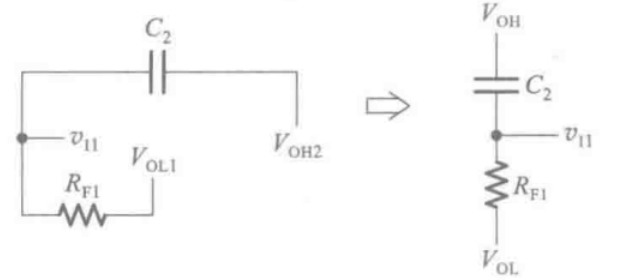
因为同时有两个电源伺候
非对称式多谐振荡器
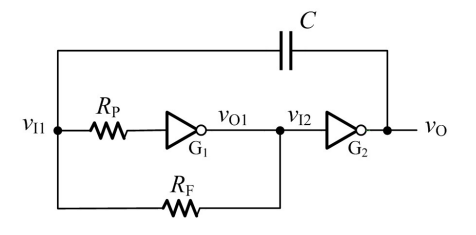
非对称式多谐振荡器如上图所示,相比于对称式,非对称式少了一个电容、一个反馈电阻,多了一个
由于某种扰动,使得
在第一个暂稳态,电容
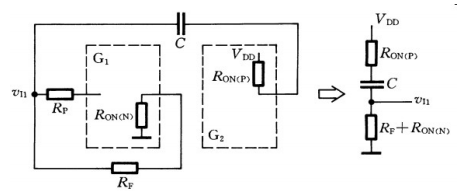
因为
这时,电容
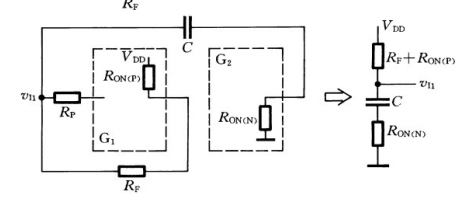
计算充电时间,有:
环形振荡电路
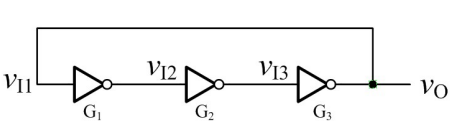
上图是基本环形振荡电路,由3个非门首尾相连构成,利用非门之间的传输延时
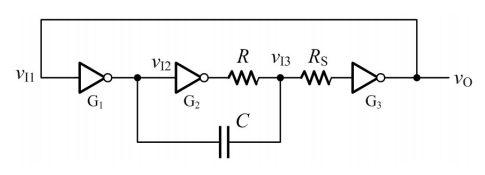
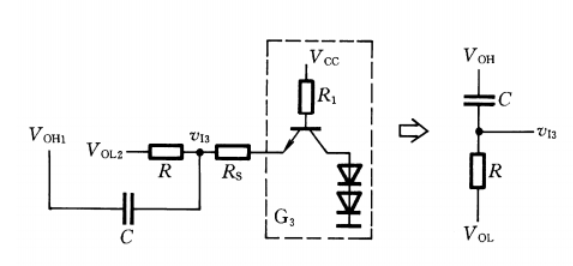
当
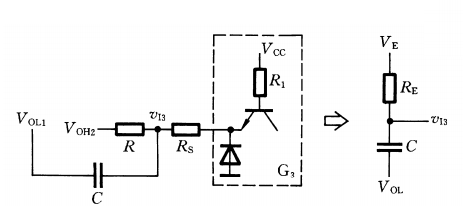
主要是由
因此,从
放电时间为:
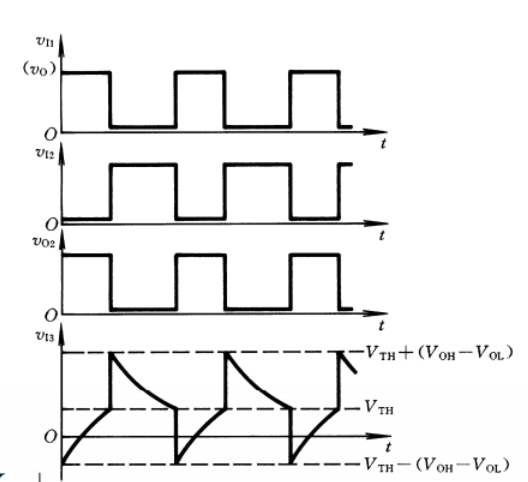
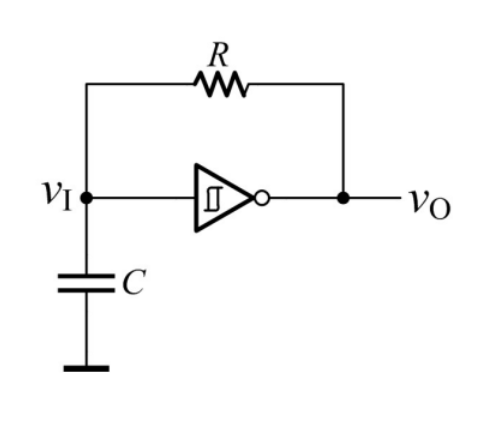
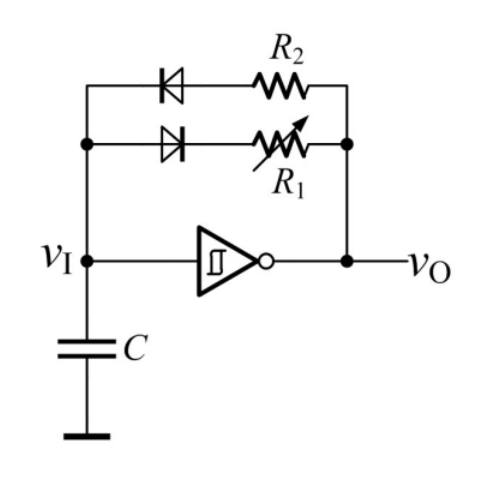
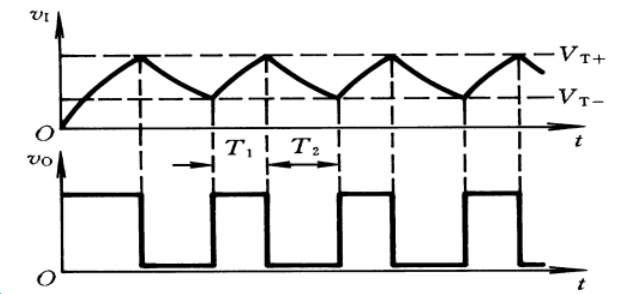
施密特触发器多谐振荡器
其原理是让电压在施密特触发器的滞回线
一开始,
波形图如下:
本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏: