微波技术·路之章

微波网络

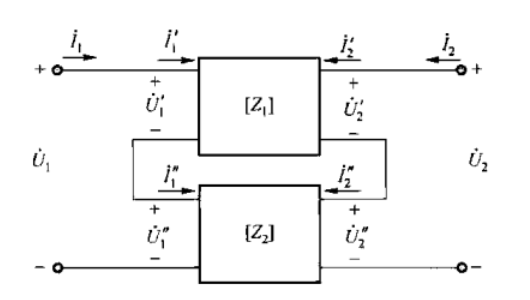
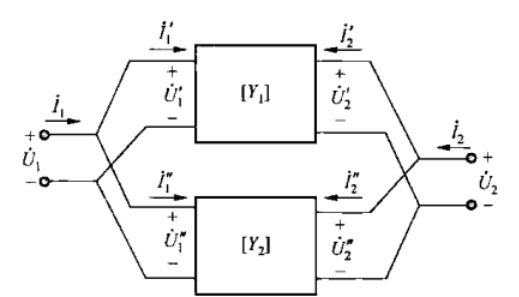
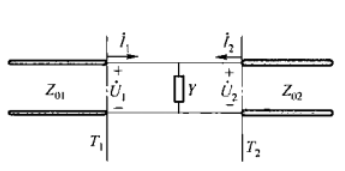
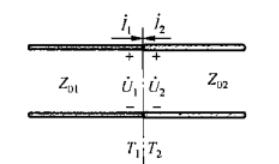
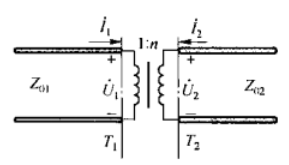
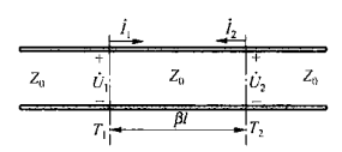
微波网络研究的对象是微波系统中的“不均匀区”（也叫微波结），如下图所示，可以由左图等效为右图分析问题

微波网络

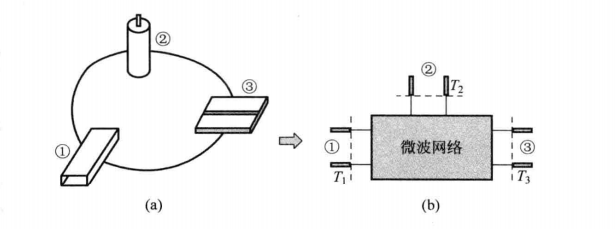
其基本思想是：把单模波导等效为双导线，把各种微波元件等效为微波网络。

单模波导等效为双导线

1. 等效复功率、电压、电流

   如果用电磁场表示的复功率，和用电压电流表示的复功率相等，有： $$\dot{P}=\frac{1}{2}{\int }_S({\dot{\overrightarrow{E}}}_{\mathrm{T}}\times {\dot{\overrightarrow{H}}}_{\mathrm{T}}^{\ast })\cdot {\hat{i}}_z\mathrm{d}S=\frac{1}{2}\dot{U}{\dot{I}}^{\ast }$$ 将电磁场纵横分离，有： $${\dot{\overrightarrow{E}}}_{\mathrm{T}}(u,v,z)={\overrightarrow{e}}_{\mathrm{T}}(u,v)\cdot \dot{U}(z)$$

   $${\dot{\overrightarrow{H}}}_{\mathrm{T}}(u,v,z)={\overrightarrow{h}}_{\mathrm{T}}(u,v)\cdot \dot{I}(z)$$

   其中$e,h$叫矢量模式函数。满足： $${\int }_S({\overrightarrow{e}}_{\mathrm{T}}\times {\overrightarrow{h}}_{\mathrm{T}})\cdot {\hat{i}}_z\mathrm{d}S=1$$

2. 等效特性阻抗$$

   设波导等效特性阻抗$$，被等效的波导模式的波阻抗$$，有： $$

3. 相位常数

   取被等效的波导模式的轴向相位常数。

不均匀区等效为网络

电路参量，也就是反映参考平面上电压和电流的关系的网络参量。

1. 阻抗参量

   由方程 $$ 得： $$ 其中$$是比例系数，称为阻抗。$$时叫自阻抗，否则叫互阻抗。 详细地来说：

   • $$表示其余端口开路时，端口$$的输入阻抗。
   • $$表示端口$$开路时，端口$$到端口$$的转移阻抗。

2. 导纳参量 $$ 即： $$ 其中的$$就是导纳参量矩阵。其物理意义为：

   • $$表示其它端口短路时，端口$$的输入导纳。
   • $$表示端口$$短路时，端口$$到端口$$的转移导纳。

归一化参量

因为反射系数是一个很直观而且容易测量的量，仿照“传输线理论”，定义归一化阻抗： $$ 于是，可以直接导出归一化电压、电流，有： $$ 即： $$ 传输线理论中所有关系式都成立，可以应用史密斯圆图.用归一化电压和电流，可以导出归一化阻抗、导纳参量。

散射参量

在传输线理论中，我们学习了入射波和反射波的概念，这是研究散射参量的出发点 。散射参量描述的是进入网络的电压波和离开网络电压波的关系。 定义$$为进入网络的归一化电压波，定义$$为离开网络的归一化电压波。

有： $$

对$$端口的微波网络，我们可以把出波表示为入波的响应，也就是线性组合的形式。 $$ 即： $$ 其中的$$就是散射参量矩阵。

在讨论散射参量矩阵的物理意义之前，首先要明确端口匹配负载和端口匹配的概念。

端口接匹配负载的意思是指端口接负载，并且所接的负载和端口传输线匹配，负载的反射波为零，即对该端口的进波为零。如果说第$$个端口接匹配负载，则$$.

端口匹配的意思是，在其它端口接负载的情况下，从该端口看进去的网络本身作为终端等效负载时和端口传输线匹配，网络反射波为零，即端口出波为零，即$$.

那么$$矩阵的物理意义是：在除了波源所在的第$$端口以外的其余各端口均接匹配负载，散射矩阵的非对角线元素$$是第$$端口到第$$端口（注意是反的）的电压传输系数，其对角线元素$$是波源所在的第$$端口的电压反射系数。

用散射参量描述网络性质

1. 互易性

   当微波元件内部为各向同性均匀媒质,即媒质极化、磁化、传导性质与外加场方向无关，进而与电磁波的传播方向无关时,其等效网络的任意两个端口都是可逆的，该网络称为可逆网络或互易网络。

   可以证明，互易网络的$$矩阵是转置不变的，即： $$

2. 无耗性

   无耗网络的$$矩阵是酉矩阵¹，即： $$

3. 对称性

   如果微波网络具有对称性，例如第$$端口和第$$端口是对称的，那么 $$

散射参量和阻抗导纳参量的转换

$$

$$

$$

$$

参考平面移动对S矩阵的影响

对于$$端口网络，各端口参考面外移长度为$$时，移动后的$$矩阵和原来的$$矩阵的关系为： $$ 其中$$是一个$$阶对角阵，满足： $$

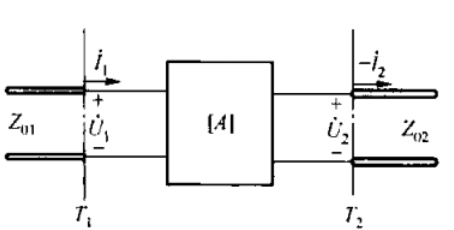
二端网络

二端网络的阻抗、导纳参量、散射参量、传输参量没有什么特别值得说的。矩阵各元素的物理意义已经在前面给出了。

二端网络的性质

• 互易性 $$

• 对称性 $$

• 无耗性 $$

  这个无耗性是从能量守恒定理出发的。如果我们把这个共轭转置展开，有以下四个式子： $$

  根据 $$ 参量物理意义有 $$ 式中, $$ 表示端口 1 输出功率大小, $$ 表示端口 2 输出功率大小, $$，表示端口 1 输人功率大小。 $$ 表示端口 1 接波源, 端口 2 接匹配负载时, 端口 1 的功率反射系数, $$ 表示此时从端口 1 到端口 2 的功率传输系数。 式 $$ 表示当端口 2 接匹配负载时, 从端口 1 输人的功率分为 两部分：一部分被系统反射 $$, 另一部分被系统传输到端口 $$ 并被负载吸收。

  式 $$ 表示当端口 1 接匹配负载时, 从端口 2 输人的能量分为 两部分： 一部分被系统反射 $$, 另一部分被系统传输到端口 $$ 并被负载吸收。

二端口网络中，有：

• 如果一个端口匹配，那么另一个端口匹配
• 如果网络完全匹配，那么完全传输

用散射参量表示网络外特性

• 电压传输系数：输出端口出波和输入端口入波之比 $$

• 插入衰减：输出端接匹配负载，输入端进波功率和输出端出波功率之比 $$ 它可以分解为两项： $$ 前一项叫吸收衰减，记作$$，由网络本身引起；后项叫反射衰减，记作$$，由输入端和外接输入线不匹配引起。

• 插入相移：出端接匹配负载，输入端进波和输出端出波相位差 $$

• 输入驻波比：出端接匹配负载，输入端测得驻波比 $$

• 回波损耗：出端接匹配负载，输入端入射波功率和反射波功率之比 $$

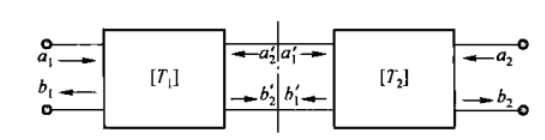
二端口网络的互联

1. 串联

   

   二端网络串联

   有： $$ 可以类比为电阻（阻抗）串联，阻值相加。

2. 并联

   

   二端网络并联

   有： $$ 可以类比导纳并联的电导等于各电导之和

3. 级联

   

   二端网络级联

   有 ： $$

转移参量

二端口网络示意图

$$ 即： $$ 其中$$称为转移矩阵，其中的各个元素称为转移参量。

归一化转移参量：把上面式子中的电压电流都换成归一化的，有： $$

转移参量和其它参量的关系：

1. 散射参量 $$ 反过来，有： $$

2. 阻抗参量 $$ 反过来，有： $$

3. 导纳参量 $$ 反过来，有： $$

至于二端口网络的各种性质，也可以用转移参量描述：

1. 互易性： $$

2. 对称性： $$

3. 无耗互易： $$

   $$

基本电路单元

1. 串联阻抗

   

   串联阻抗

   转移矩阵： $$ 归一化： $$

2. 不同阻抗的传输线相连

   

   不同阻抗的传输线相连

   转移矩阵： $$ 归一化转移矩阵： $$

3. 理想变压器：

   

   理想变压器

   转移矩阵： $$ 归一化： $$

4. 一段均匀传输线：

   

   均匀传输线

   转移矩阵： $$ 归一化： $$

无耗三端口网络

具有以下性质：

1. 无耗互易三端口网络不可能完全匹配。如果端口1、2匹配，那么端口3和网络完全隔离，即$$
2. 任何完全匹配的无耗三端口网络一定是非互易的。
3. 对称互易无耗的三端口网络，输入驻波比不低于2
4. 无耗互易三端口网络中任意端口接短路活塞，总可以找到活塞的一个位置，使其它两个端口互相隔离。
5. 如果无耗互易三端口网络对于接有短路活塞的端口是对称的，则总可以找到活塞的一个位置，使其它两个端口之间可以无耗的传输。

无耗四端口网络

具有以下性质：

1. 如果一个无耗互易四端口网络的任意三个端口匹配，则第四个端口自动匹配，且该网络构成一个定向耦合器。所谓的定向耦合器是指对四端口元件，当某个端口接波源、其余端口接匹配负载时，必然和其中一个端口理想隔离。理想定向性要求接波源的端口无反射，即输入端口匹配。
2. 有理想定向性的无耗互易四端口网络不一定四个端口都匹配。
3. 有两个端口匹配且互相隔离的无耗互易四端口网络一定是完全匹配的定向耦合器。

微波元件

一端口元件

1. 短路负载

   扼流式短路负载的基本原理是：利用传输线的$$波长阻抗变换特性，把有高频电流流过，需要良好电接触的地方，恰好安排在电压波节点（电流波腹点）处，从而得到等效短路。

2. 匹配负载

   它可以几乎无反射地吸收入射波的全部功率，在传输系统中建立行波状态。

3. 失配负载

   它具有某一个固定的驻波比，在微波测量中作为标准终端负载。

二端口元件

1. 波导接头

   是用来把传输线接在一起的。有平接头、扼流接头等。

   

   波导接头

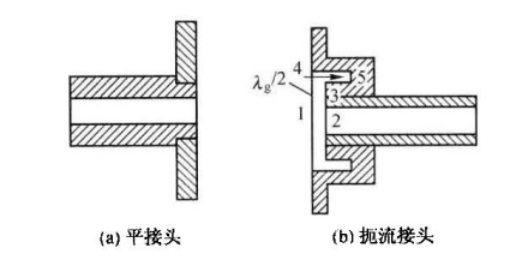
   扼流接头在连接波导的法兰盘上有一个深为$$的槽，这样可以保证接头处恰好是电流波腹点。

2. 拐角、弯曲、扭转元件

3. 调配元件

   是一些电抗元件，放在传输线上，产生附加反射，使得传输线匹配。

   1. 电抗膜片：分为感性膜片、容性膜片、谐振窗
   2. 销钉
   3. 螺钉匹配器

4. 衰减器

   吸收式衰减器散射矩阵： $$ 截止式衰减器：插入一个比较小的传输线，使得电磁场在这一小段里面截止。其特点有：

   1. 衰减量dB和距离呈线性关系
   2. 当$$，衰减系数$$很大，移动较小的距离就可以得到很大的衰减量
   3. 衰减是由于反射产生，输入端和输出端严重失配

   还有极化衰减器

5. 相移器

   其S矩阵为： $$

---

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

---

1. 酉矩阵也叫幺正矩阵，即它的共轭转置和它的乘积是单位矩阵。↩︎