数字信号处理·傅里叶之章

你说得对，但是《数字信号处理》是电子信息工程学院独立开设的一门核心专业课，课程发生在一个被称作D221的幻想世界，在这里，被神选中的序列将被授予“傅里叶变换”，导引频域分解之力。玩家将扮演一位名为“DSP”的神秘角色，在自由的系统中邂逅性格各异、能力独特的信号们，和他们一起分析频谱，找回失散的频段——同时，逐步发掘“线性系统”的真相。

离散傅里叶变换DFT

我们之前已学过很多“变换”了，例如连续时间信号傅里叶变换FT、连续时间信号傅里叶级数FS、离散时间序列傅里叶变换DTFT、离散时间序列傅里叶级数FS。

各个变换

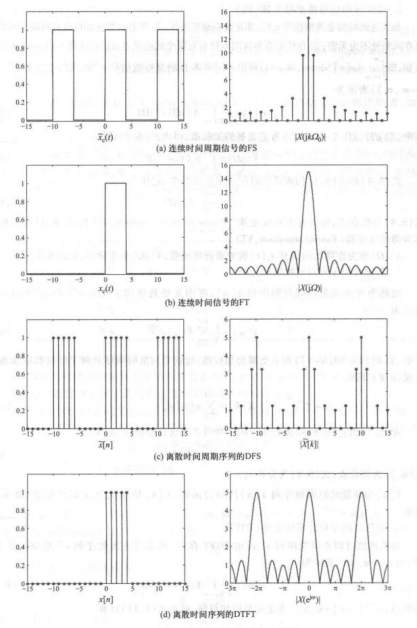
因为数字系统只能处理离散序列，而这其中只有DFS同时在时域和频域是离散的。但是DFS又是周期无限长序列，而现有的数字系统仍然不能实现。因此我们必须考虑用有限长序列建立时域离散和频域离散的关系。

设$$是周期为$$的周期序列，那么称 $$ 为“主值序列”，也就是原序列的第$$个值。

设$$是长度为$$的有限长序列，那么为了将其周期性延拓，有： $$

记作： $$ 其中$$称作取模运算，设$$，则$$。

周期序列$$可以看作有限长序列$$的周期延拓，因此只需计算主值区间中的DFS，即可对周期序列进行恢复。有DFT的定义： $$ 我们可以看出：DFT并不是一个新的变换形式，而是DFS在实频域的主值序列，因此其很多性质和DFS有类似性。

几大变换之间的关系

以下：将Z变换记作$$，将DTFT（离散时间序列傅里叶变换）记作$$，将DFS（离散时间序列傅里叶级数）记作$$，将DFT（离散傅里叶变换）记作$$。

Z变换和DTFT

$$的DTFT是其Z变换在单位圆上的采样。即： $$

DTFT和DFS

对$$在$$的等间隔频率点进行$$点采样得到周期序列$$。对$$作IDFS（离散时间序列傅里叶级数逆变换），得到序列$$。

由： $$ 和 $$ 把上式带入下式，有： $$ 有复指数函数的正交性和周期性，有： $$ 可以看到，$$是$$的周期移位。也就是说，正如时域采样会导致频域周期延拓，频域采样也会导致时域周期延拓。下面按$$的长度$$和频域采样数$$分情况讨论：

1. 非周期序列$$不是有限长序列，则频域采样一定会造成混叠
2. $$时，仍会产生时域混叠失真。混叠的长度就是$$，参考上面的式子
3. $$时，才能由频域采样$$恢复出$$

DFS和DFT

如前文所说，DFT和DFS本质上来说是一种变换，不过DFS的离散时间序列是周期的，变换得到的频域也是周期的，DFT是DFS的主值序列。

DFT的性质和定理

在研究DFT的性质时，需要时刻注意DFT的有限定长度性以及循环周期性。当涉及到两个长度不同的序列时，要通过补0的方式使其长度均为$$。

1. 线性

2. 时域循环位移性质

   这里的循环移位是圆周移位，在序列中，从左（右）边移出多少位，就会从右（左）边移入相同位的序列值。 $$

3. 频域循环位移性质 $$

4. 时间倒置性质 $$

5. 此外，还有实频域循环卷积、对偶、帕塞瓦尔等性质。

DFT的对称性

和DFS的基本相同。重点是：DFT的对称都是“圆周对称”。对于圆周共轭对称序列，有： $$ 对于圆周共轭反对称序列，有： $$ 如果$$是实信号，那么它的DFT$$是圆周共轭对称的。也就是说它的实部$$是圆周偶对称，虚部是圆周奇对称。

用DFT实现线性卷积

这是我们之前几章经常用的线性卷积： $$ 这是我们DFT里经常用的N点循环卷积： $$ 把$$ 带入，有： $$ 于是，我们可以证明：循环卷积的结果是线性卷积以$$为周期的周期延拓的序列的主值序列。因为线性卷积序列的长度是$$，于是循环卷积的点数必须满足$$时，才不会发生混叠，取主值序列时才满足$$

根据上述推理，我们可以利用DFT来实现卷积，计算框图如下：

DFT实现线性卷积

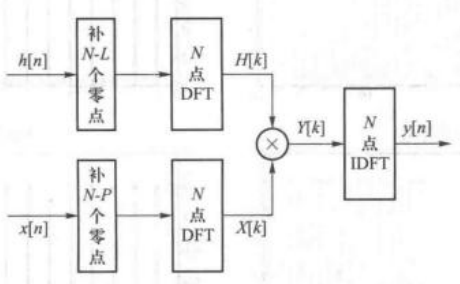
DFT实现线性系统（块卷积方法）

在实际的操作中，输入序列$$的长度远远大于冲激响应$$的长度$$，所以计算效率比较低，所以需要分段处理，把输入序列分成长度为$$的块，再进行计算。有两种方法，分别是重叠相加法和重叠保留法。

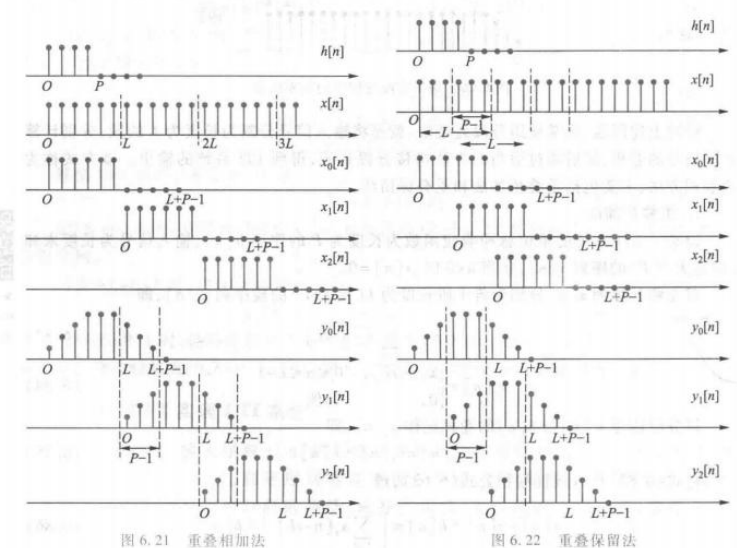
重叠相加法：

把输入序列按顺序直接切割成若干个长度为$$的段序列$$，即： $$ 对每个分段信号，和$$进行线性卷积： $$ 其中$$是长度为$$的序列。由卷积的性质，有： $$ 则： $$ 也就是说，尽管相邻两段$$会有重叠部分，但是加的时候不要管，直接叠加就行了。所以，这种方法叫做重叠相加法。

重叠保留法：

重叠保留法在对$$分割成$$时，两个相邻的$$之间存在$$长度的重叠，即： $$ 有： $$ 把每个序列段和$$的线性卷积记作$$则： $$ 意思是，在拼接时，每个$$序列都应该去掉$$和$$的部分。但是，明明拼接时去掉了一部分，为什么要叫“重叠保留”呢？哈哈。

块卷积方法

快速傅里叶变换FFT

一般的DFT，其时间复杂度是$$，难以处理很长的数据。FFT把计算复杂度降低到了$$次，大大提高了计算效率。FFT的实质是分治算法，把一个长度为$$^[1]的序列不断地分拆成长度为$$，再利用旋转因子$$（即$$）的性质由子序列的DFT来合成整个序列的DFT。

时间抽取（DIT）FFT

时间抽取FFT

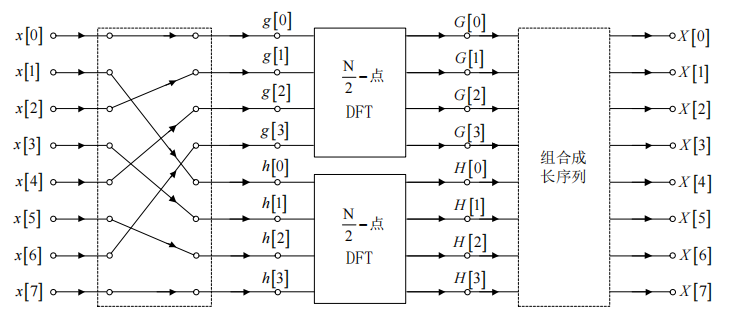
这是DIT-FFT的基本框图。把长度为$$的序列$$按奇偶分为两个长度为$$的序列$$。接下来我们来推导“组合成长序列”这一步究竟是如何进行的。

由傅里叶变换定义式： $$ 把$$分解为奇数偶数两部分： $$ 把等式右侧的$$分解开，有： $$ 再回忆一下傅里叶变换的定义： $$

$$

我们惊喜地发现：可以代换了。有： $$ 只要再注意到$$都是以$$为周期的，那么“组合成长序列”的方法已经昭然若揭了：

组合成长序列

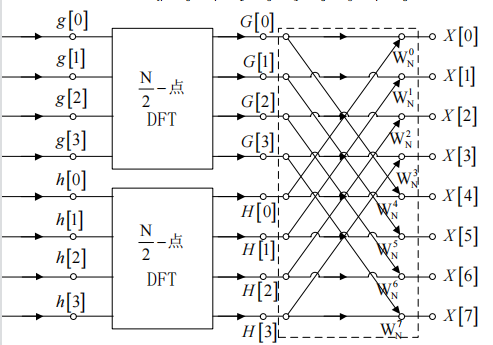
当然，这个图还可以继续优化，只需要注意到： $$ 有：

优化

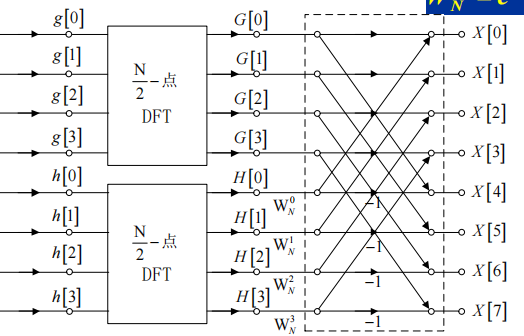
接下来如法炮制，对$$进行分析，把它们分解为$$的序列，进行计算，直到序列的长度只有2为止。此时，有：

序列长度只有2

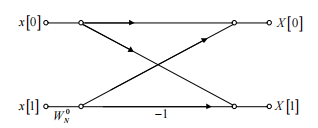
我们得到了计算这个长度为8的序列的FFT的全过程流图：

全过程流图

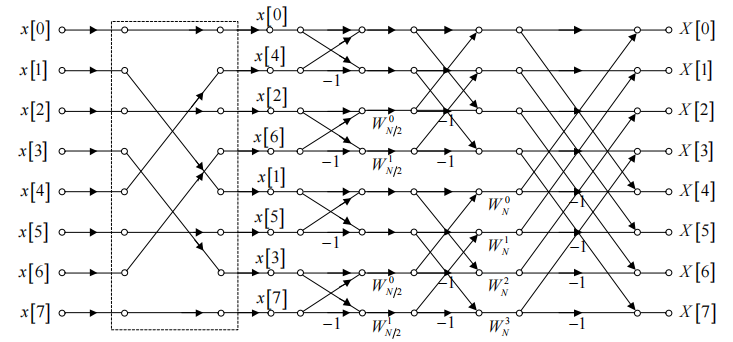
按频率抽取（DIF）FFT

按频率抽取

仿照上面的过程，我们来推导“组合成短序列”的过程。由DFT的定义： $$ 把它拆开： $$ $$ $$ $$ $$ $$

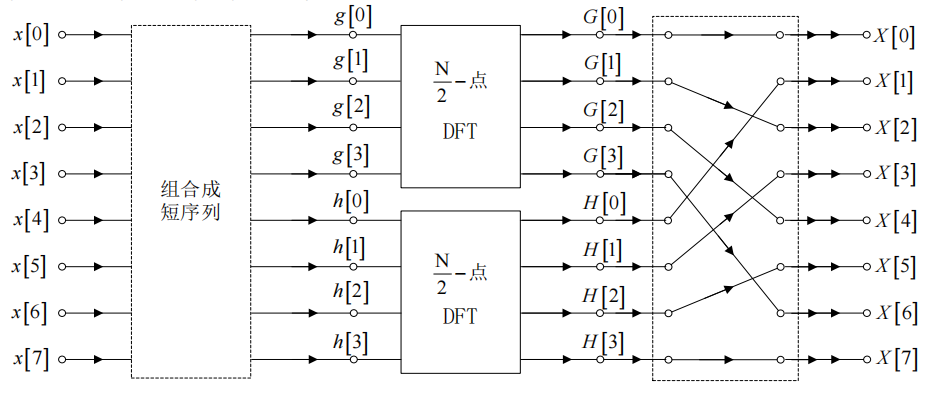
$$ 于是，我们可以画出流图：

DIF流图

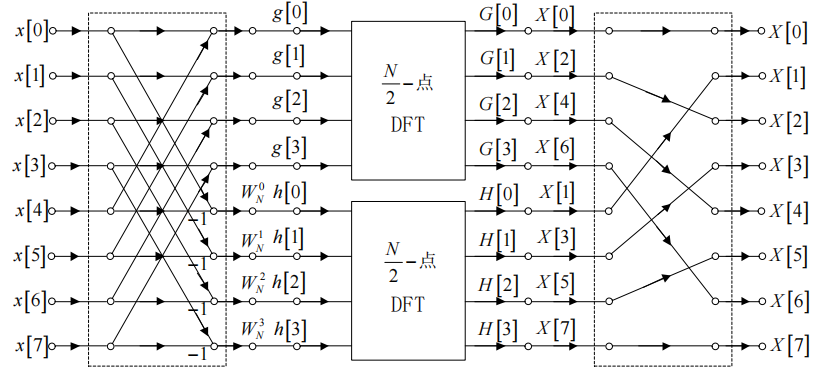
如此重复，直到序列长度为2，有：

长度为2的流图

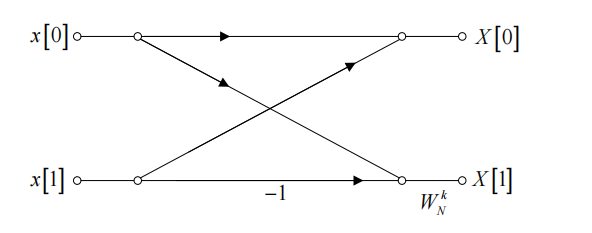
于是，全过程流图为：

DIFFFT全过程流图

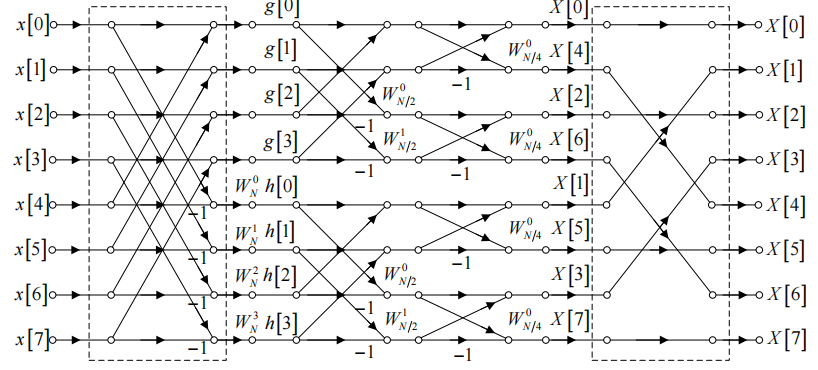
IFFT

在不修改电路（程序）的情况下，直接借用FFT的模块实现IFFT，有两种操作方法。

1. 把蝶形运算中的旋转因子$$换成$$，把$$送进输入端，对输出的结果除以$$
2. 把$$送入输入端，计算输出的共轭，然后除以$$

实数序列的FFT

前面所提到的序列都是复序列。如果要计算实数，当然可以把它当成虚部为零的复数，但是也有更简便的计算方法。

N点FFT计算两个N点实序列

构造复序列$$，则有： $$

$$

N点FFT计算2N点实序列

构造复序列$$，其中$$是原实序列的偶数项，$$是原实序列的奇数项。则有： $$

$$

$$

---

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

1. 在本节中，进行FFT的序列长度默认为2的整数次幂，不足则用0补齐。 ↩︎