数字电路·逻辑之章

[toc]

你说得对，但是《数字电子技术基础》是电子信息工程学院独立开设的一门核心专业课，课程发生在一个被称作五（203）的幻想世界，在这里，被神选中的信号将被授予“门电路”，导引高低电平之力。玩家将扮演一位名为“学生”的神秘角色，在自由的课程中邂逅性格各异、能力独特的元件们，和他们一起分析逻辑，找回失散的导线——同时，逐步发掘“Verilog”的真相。

数制和码制

数制

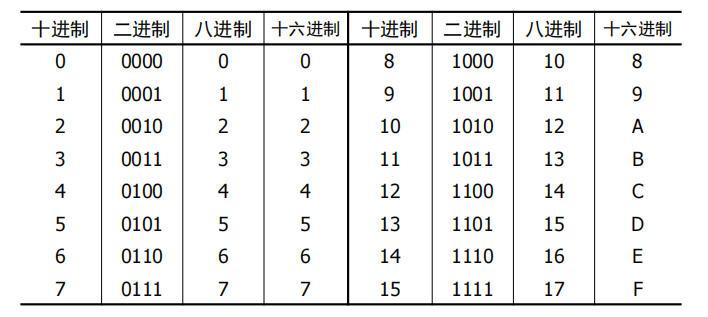
数制指的是数字每一位的构成方法，以及从低位到高位的进位规则。常用的数制有十进制、二进制、八进制、十六进制。

k进制数字的基本表示方式为： $$(\cdots x_2{x}_1{x}_0.x_{-1}{x}_{-2}\cdots {)}_k=\sum _{i=-\mathrm{\infty }}^{\mathrm{\infty }}{x}_i\times k^i$$

不同数制的转换方式

• 任意进制到十进制的转换

  直接按上面的式子展开即可。

  【例】$$

• 十-二转换

  整数部分用除二取余法，小数部分用乘二取整法。这成天写，我不展开了，忘了就随便拿个什么11啊这种数字推一下。

• 二-十六（八）转换

  分组对应法最快。

  

  进制转换对应表

不同进制下四则运算的规则和方法和十进制一致。

原码、反码和补码

• 原码

  最高位（最左边的一位）表示正负号，0为+，1为-，其余各位表示数的绝对值。

  表示范围为$$，0的表示不唯一

• 反码

  正数和原码的规则一样，有符号位和绝对值；负数是它的相反数整体（含符号位）取反，当然也可以理解成，负数的符号位是1，绝对值按位取反。

  表示范围为$$，0的表示不唯一

• 补码

  正数和原码的规则一样；负数为“反码加一”，即符号位为1，绝对值按位取反，再加一。

  表示范围为$$，0的表示唯一。

  补码加减法运算，符号位参与运算，而且应该在相应位数表示的数值范围内进行，进位直接丢弃。

  【例】利用补码加法计算39-22

  【解】$$，两个二进制数相加后为$$，舍弃溢出位，得结果为$$

  补码的运算有模的特性。

码制

• BCD码

  BCD码，即二-十进制代码，它是用二进制代码表示十进制数码的编码方法，也就是0~9这十个符号的二进制编码。分为恒权码和变权码等。

  例如：8421码，就是从高位到低位的权依次是8421（和普通二进制一样），它的有效编码是0000_{1001，分别代表0}9，其它的是非法码。

  还有其他的编码，比如2421码、余3码、余3循环码等。

  

  常用BCD码

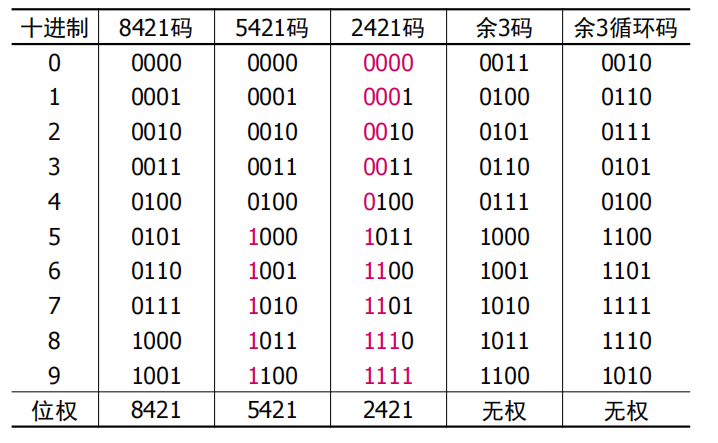
• 格雷码

  格雷码的特性如下：

  • 单位距离：相邻码字仅有一个位元不同，其它位都相同。
  • 循环相邻：对于n位循环码，如果从第0个码字开始，最大范围是第$$个码字，而对$$的编码一定是$$的自然二进制码。
  • 镜像反射

逻辑代数

逻辑运算的大部分知识已经在“离散数学”课程中讲过了，这里仅进行补充。这里“$$”表示与，"$$"表示或，$$表示非，$$表示异或，$$表示异或。

逻辑函数的两种标准形式

两种标准形式就是指标准与或表达式（也叫最小项之和，主析取范式），和标准或与表达式（也叫最大项之积，主合取范式）。

• 标准与或表达式

  形如下列式子的形式： $$ 这三个形式都是标准与或表达式。$$下面的下标由对应的最小项确定（没有取反的项记为1，有取反的项记为1，构成一个二进制串，转换为十进制即可）。

• 标准或与表达式

  形如下面的式子： $$ 和上面的一样，不赘述了。

逻辑化简

公式法略。

卡诺图法

卡诺图法是一种从真值表出发得到最简与或表达式的方法。使用卡诺图的步骤如下：

1. 先记住这几个标准格式

   

   卡诺图

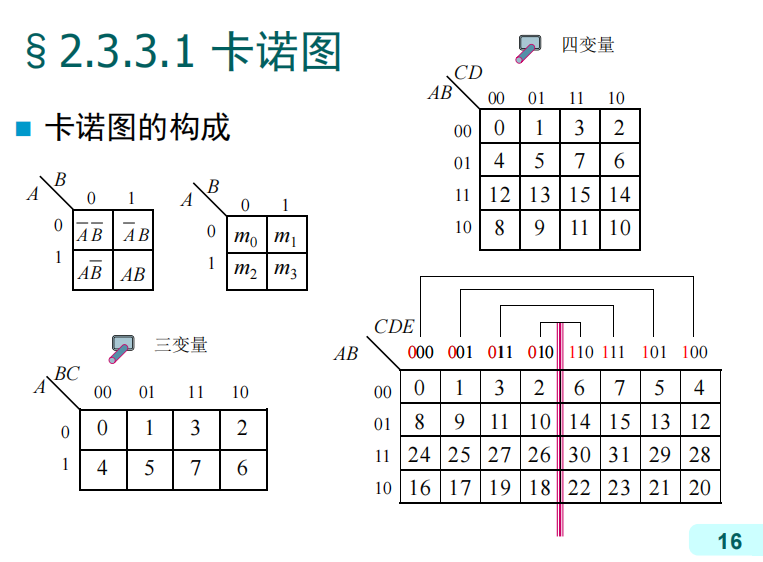
   其实很好记的，横纵坐标就是格雷码的顺序，这也是为了利用单位距离性。

2. 在逻辑函数为真的格子上填1，逻辑函数为假的格子填0

3. 画卡诺圈（乘积项），合并最小项（1），反复利用互补律化简。卡诺圈的形状可以是日字形，田字形，而且有循环边界条件。

   互补律：$$

   画卡诺圈时应该遵循以下原则：

   1. “1”格不能漏圈
   2. “1”格可以属于一个以上的圈
   3. 圈越大越好
   4. 圈越少越好
   5. 每个圈应该包含至少一个新的“1”格

无关项

有时候，输入逻辑变量的某些取值组合禁止出现，这种叫做“约束项”。有时候，一些取值组合出现时，输出逻辑值可以是任意的，这种叫做“任意项”。以上两个统称为无关项。在化简时，把无关项用X表示，在画卡诺圈时，X既可以被当作1，也可以被当作0，具体看你需要。

逻辑函数形式的转换

除了我们前面说的最简与或式以外，还有一些常用的形式。

• 最简或与式

  在画出$$的卡诺图后，合并$$方格，求反函数的最简与或表达式，然后使用德摩根公式进行反演变换，得到原函数的最简或与表达式

  德摩根公式： $$

  【例】已知Y的反函数，求Y的最简或与式。 $$ 【解】 $$

• 或非-或非式

  先求出最简或与式，对最简或与式求两次反，再对内侧（下面）的反用一次德摩根公式展开。

  【例】 $$

  也可以在求出反函数的最简与或表达式的时候，直接对反函数两端求反，再对各个乘积项用德摩根公式

  【例】 $$

• 与非-与非式

  把与或表达式两次取反，再用德摩根公式即可。

  【例】 $$

• 与或非式

  先求反函数的最简与或表达式，再求反。

  【例】 $$

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：