微波技术·波之章

你说得对，但是《微波技术》是电子信息工程学院独立开设的一门核心专业课，课程发生在一个被称作五（303）的幻想世界，在这里，被神选中的信号将被授予“波导”，导引电磁波。玩家将扮演一位名为“传输线”的神秘角色，在自由的课程中邂逅性格各异、能力独特的圆图们，和他们一起分析阻抗，找回失散的能量——同时，逐步发掘“Black Magic”的真相。

[toc]

传输线理论

微波的工作频率为$300MHz\sim 3000GHz$，对应的自由空间中的波长为$1m\sim 0.1mm$，在这种条件下，日常尺度的导线以及具备很多异于理想导线的性质，被称作“长线”或者“传输线”，理想导线则被称作“短线”。具体来说，当系统的电长度$l/\lambda \ge 0.05$时，就要用传输线理论来分析问题，这种导线就被称作长线。

传输线方程

对于传输线上的一个微元$dz$，有其等效集总参数模型：

image-20221118153336875

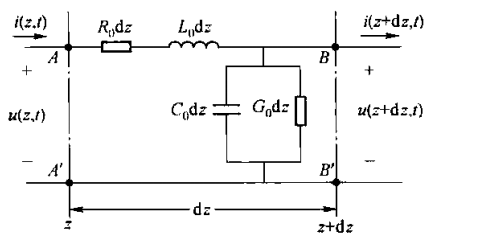
其中$$叫分布电阻，$$叫分布电感，$$叫分布电导，$$叫分布电容。理想导体的$$，理想介质的$$。

根据基尔霍夫定律列出方程，转换为复频域形式，则有我们所说的传输线方程，也叫频域电报方程 $$ 其中$$叫单位长度串联阻抗、$$叫单位长度并联导纳。把上面两个式子对$$求导，再代换，有： $$ 其中 $$ 叫做传播常数，是一个取决于传输线物理性质的常数。于是，可以解出传输线方程的通解： $$

$$

其中$$叫做传输线特性阻抗，有： $$ $$是待定常数，要根据端口条件来确定。

完整电路

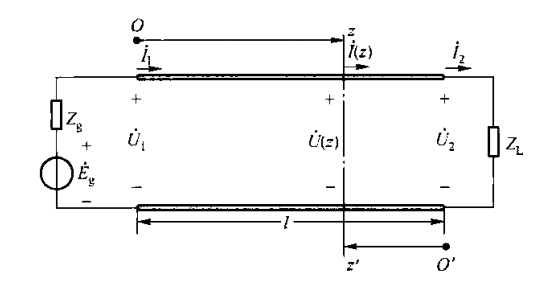
1. 终端条件

   即已知终端$$。则有： $$

2. 始端条件

   即已知$$。则有： $$

3. 波源阻抗条件

   即已知$$，有： $$

传输线上的参量

一次特征参量

$$分布电阻，$$分布电感，$$分布电导，$$分布电容

二次特征参量

二次特征参量也叫传播特性参量，其中最主要的就是传播常数$$和特征阻抗$$，具体的计算式已经在上面给出了。还有一些其它的特征参量，可以由上面的导出。

1. 衰减常数和相位常数

   若$$，那么$$叫做衰减常数，表示经过单位长度行波幅度衰减$$，$$叫做相位常数，表示单位长度行波滞后的幅度。对于无耗传输线，有： $$

2. 相速度和相波长

   相速度就是等相位面移动的速度，相波长就是等相位面在一个周期内移动的距离。有： $$

   $$

   对于均匀无耗传输线，有： $$

   $$

3. 特性阻抗

   特性阻抗具有如下特点：

   • 同一时刻，传输线上行波电压不同，但是传输线上各点的入射波电压和入射波之比是一个定值，这个值就是特性阻抗
   • 传输线特性阻抗仅取决于传输线的结构，和其长度无关
   • 特性阻抗描述入射（或反射）波电压和电流的幅度相位关系。

工作状态参量

1. 反射系数

   定义电压反射系数： $$ 电流反射系数可类似定义，但我们一般都用电压反射系数。

   对于无耗传输线，有： $$ 若终端负载处反射系数为$$，则有： $$ 其中$$是$$的相角。

2. 输入阻抗

   输入阻抗是传输线上任何一点的总电压和总电流的比，即： $$ 输入阻抗和线上反射系数可以互相转化： $$

   $$

   需要提醒：上面两个式子对终端也适用，也就是说如果终端直接接入阻抗$$，是可以直接计算终端反射系数$$的。进一步，有： $$ 当然，我感觉这个用史密斯圆图更好算。

驻波参量

当$$时，称传输线阻抗匹配，否则称传输线失配。我们用驻波参量来衡量失配程度。

1. 驻波比SWR（$$）

   驻波比的定义是沿线电压最大值和最小值之比，它和反射系数是一一对应的。对于无耗传输线，有： $$ 当完全匹配时，驻波比为1，沿线电压最大值和最小值相等，$$。

2. 行波系数$$

   就是驻波比的倒数。

3. 驻波相位$$

   离终端最近的电压波节点到终端的距离

无耗传输线上的波有三种传输模式：

1. $$，此时阻抗匹配，波形是行波
2. $$ 开路、短路或是纯虚数，此时传输线处于全反射状态，波形是纯驻波。
3. 其它情况，传输线处于部分反射状态，波形是行驻波。

史密斯圆图

归一化阻抗和导纳

定义归一化阻抗： $$ 则有： $$ 再定义归一化电标度（电尺寸）： $$ 则有： $$ 表达式中不再包含和传输线结构有关的参量，于是此表达式可以适用于任意传输线的分析。

由阻抗和反射系数的一对一转换关系： $$ #### 阻抗圆图

把$$平面转换到$$平面，可得阻抗圆图：

image-20221123104650102

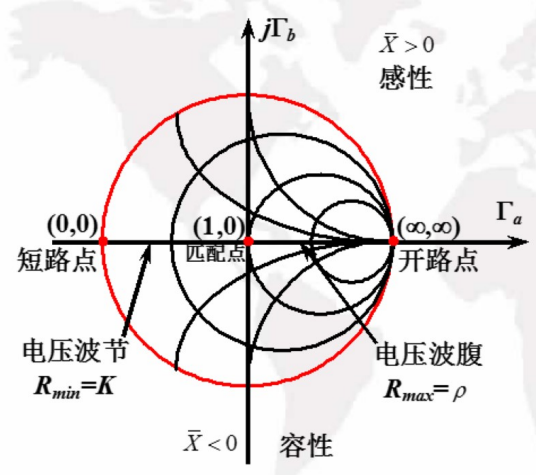
图中有三个关键点：

1. 匹配点：$$点，对应$$点，此时有$$，传输线匹配，驻波比为1
2. 开路点：$$点，对应$$点，此时$$，传输线处于开路状态，驻波比无穷大
3. 短路点：$$点，对应$$点，此时$$，传输线短路，驻波比无穷大

三个圆：

1. 等电抗圆：指的是圆心在直线$$上的那些圆，在一个等点抗圆上的点有相等的电抗。在上半平面的电抗大于零，叫做感性；在下半平面的电抗小于零，叫做容性。其圆心在$$，半径为$$。$$越小，等电抗圆越大。当$$时变成横轴，当$$时变成开路点。

2. 等电阻圆：指的是圆心在实轴（横轴）上的那些圆，在一个等电阻圆上的点有相等的电阻。其圆心为$$，半径为$$。$$越小，等电阻圆越大。

3. 等反射系数圆（也叫等驻波比圆）：指的是圆心在$$的圆。圆的半径和反射系数以及驻波比有一一对应关系。当反射系数为正实数（即在实轴正半轴）时，对应电压波腹点，于是实轴正半轴叫做电压波腹线；同理，实轴负半轴叫做电压波节线。

   当在传输线上移动$$时，对应沿等反射系数圆旋转一圈，方向为“源顺负逆”。

于是，在圆图中任意确定一个点，总能找到一个等电抗圆和一个等电阻圆与之对应，这样一来，我们就能读出这个点的阻抗。要确定传输线上其它点的阻抗，只需要按照源顺负逆的规则，在等反射系数圆上进行移动即可。

导纳圆图

把阻抗圆图以圆心为中心旋转180度就是导纳圆图。在阻抗圆图中确定一点，绕等反射系数圆旋转180度，反射系数变为$$。则$$处在阻抗圆图中读出的归一化阻抗值就是原位置$$处的导纳值。

旋转时，波节线、波腹线、短路点、开路点随之旋转。但是“源顺负逆”的准则不变。

在导纳圆图上确定归一化导纳时，有关系： $$

阻抗匹配技术

阻抗匹配包含两种含义，其一是信号源的匹配，即想办法从信号源中获得最大的功率并消除信号源的反射；其二是负载的匹配，即想办法消除反射。阻抗匹配有三种：信号源阻抗匹配，负载阻抗匹配，共轭阻抗匹配。其重要性有：

1. 负载匹配时功率最大，功率损耗最小

2. 阻抗匹配可以改善系统信噪比

3. 功率分配网络中的阻抗匹配可以吉昂蒂幅度和相位的误差

4. 保持信号源工作稳定性

5. 提高传输线 的功率容量 $$

$$匹配

是一段特征阻抗为$$，长度为$$的传输线。如果这段传输线末端接$$阻抗，那么可以计算出，这部分的输入阻抗为： $$

推导过程：由公式 $$ 把$$代入，得$$，此时可以把$$项略去，并把$$项约分掉，就得： $$

这个结论也叫“$$传输线阻抗变换特性”，需要记住。

得 $$ 如果负载不是纯电阻，那么可以把匹配器接在电压波腹点$$或电压波节点$$。此时，匹配的目的是要把输入阻抗变成纯电阻。匹配时，首先确定负载所在的等反射系数（等驻波比）圆，然后在这个圆上确定波节点/波腹点，读出对应的电阻值。负载的点和波节/波腹点的电标度的差决定了$$传输线的位置（这个位置指的是从负载到$$传输线最近的边缘的距离），在这里放置$$传输线，其到负载之间的部分（负载+原传输线）等效为纯阻。然后，再把这个纯阻（刚刚读出来的）带入前面的方程中，计算$$传输线所需的阻抗。

四分之一波长匹配器匹配过程

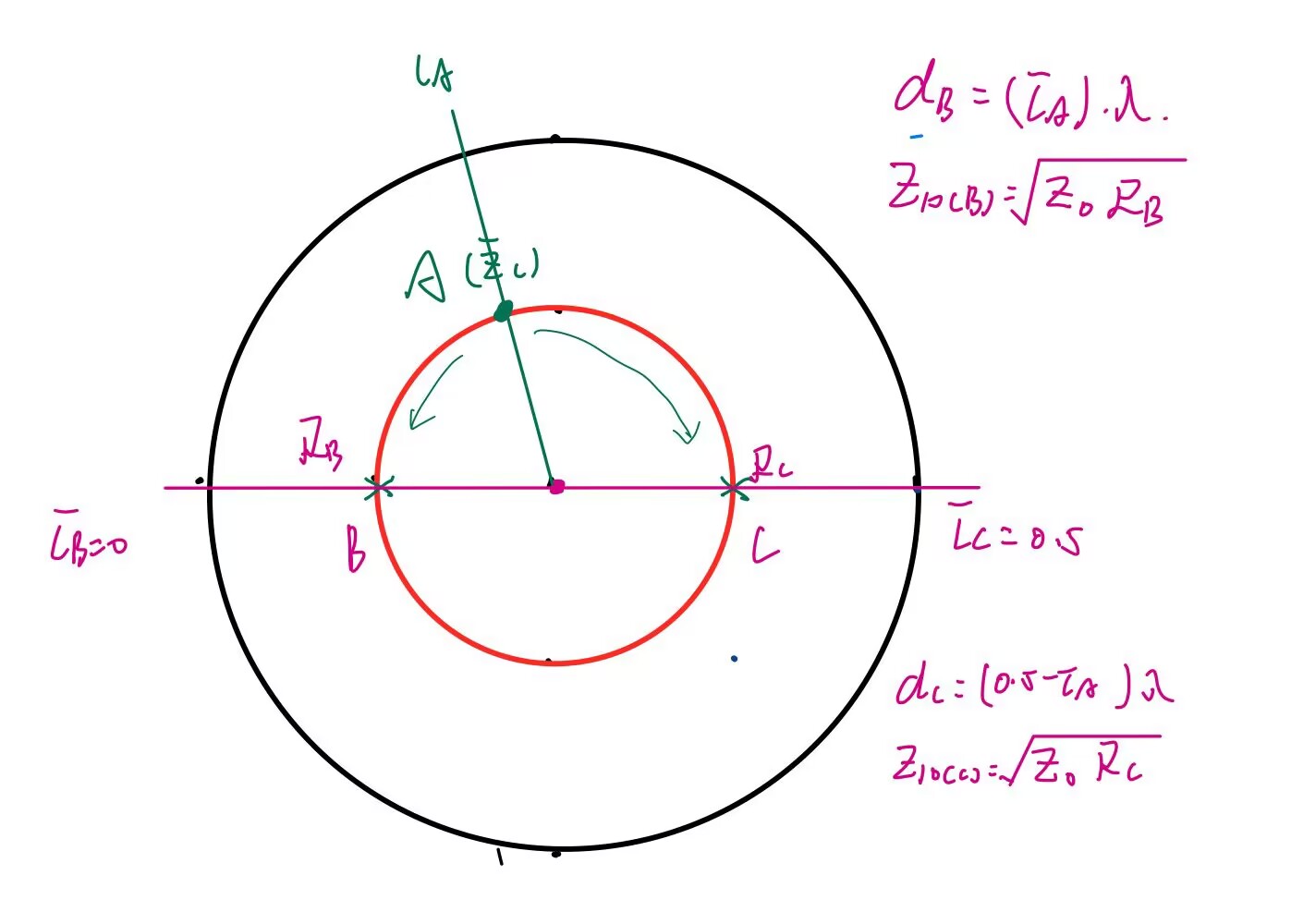
单支节匹配

单支节匹配是在传输线上并联一根传输线枝节，通过调节枝节的位置$$和长度$$，抵消阻抗的虚部，从而实现匹配。其步骤为：

1. 在史密斯圆图上画出归一化负载阻抗$$的位置，把它旋转180度，画出归一化负载导纳$$的位置，把导纳的位置记作$$，电标度为$$

2. 首先来求$$：从$$点开始，沿着等反射系数圆顺时针旋转，直到和可匹配圆（$$）相交，交点记作$$，对应导纳$$，则在此位置并联$$的电纳即可实现匹配。设$$点的电标度为$$，则有： $$

3. 接下来求$$：找到短路点（圆图右侧端点）位置，其电标度为0.25.从短路点开始，顺时针沿着全反射圆移动到电纳值为$$的地方，记作$$点。$$点的电标度为$$，则有： $$

以上过程可由如下图示描述，不同颜色表示不同的步骤：

单枝节匹配过程

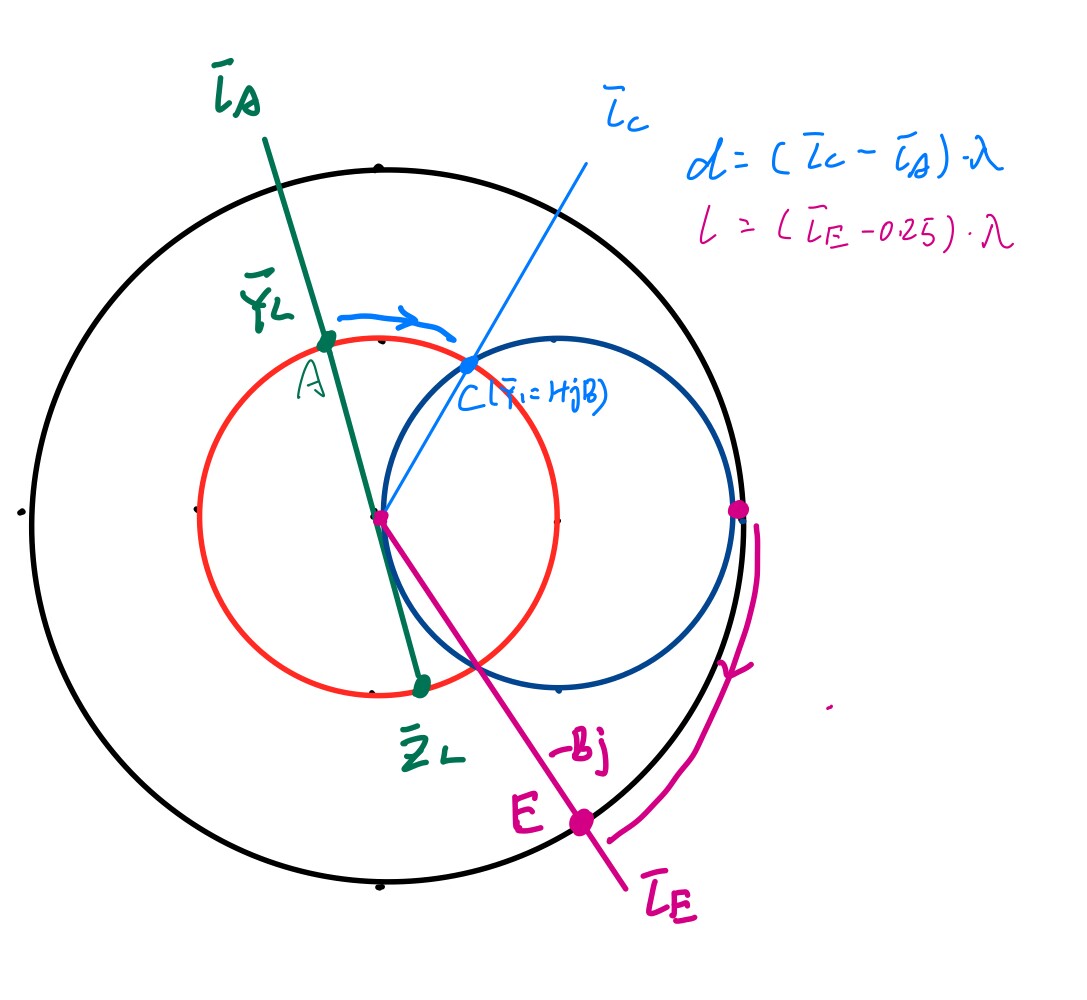
双支节匹配

在单支节匹配中，我们移动枝节的位置，来寻找归一化电导值为1的参考面。那么有没有别的办法得到这个面呢？有：我们在枝节和负载中间附加一个纯电纳即可。

双支节匹配示意图

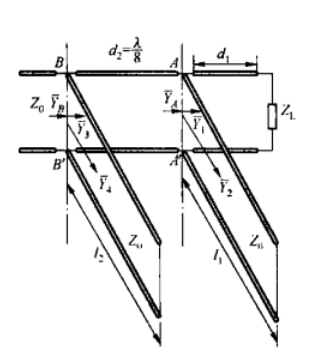
如图所示，这两个枝节的位置是固定的，我们首先要调节$$的长度，让$$号支节所在的参考面的归一化电导值为1，然后再调节$$的长度，以达到匹配效果。

以下，记：

名称	含义	备注
$$	$$段传输线（含负载）归一化输入导纳
$$	$$号支节始端归一化输入导纳	纯纳
$$	$$段传输线始端归一化输入导纳	在可匹配圆上
$$	$$号支节始端归一化输入导纳	纯纳
$$	整个系统最前端等效负载归一化导纳	$$
$$	$$段传输线终端等效负载归一化导纳	$$

于是，我们知道：$$在可匹配圆上，由于$$传输线会对于每个$$对应的点有一个绕着圆心旋转的作用，所以我们把可匹配圆也绕着圆心旋转$$，称作“辅助圆”。双支节匹配的过程是：

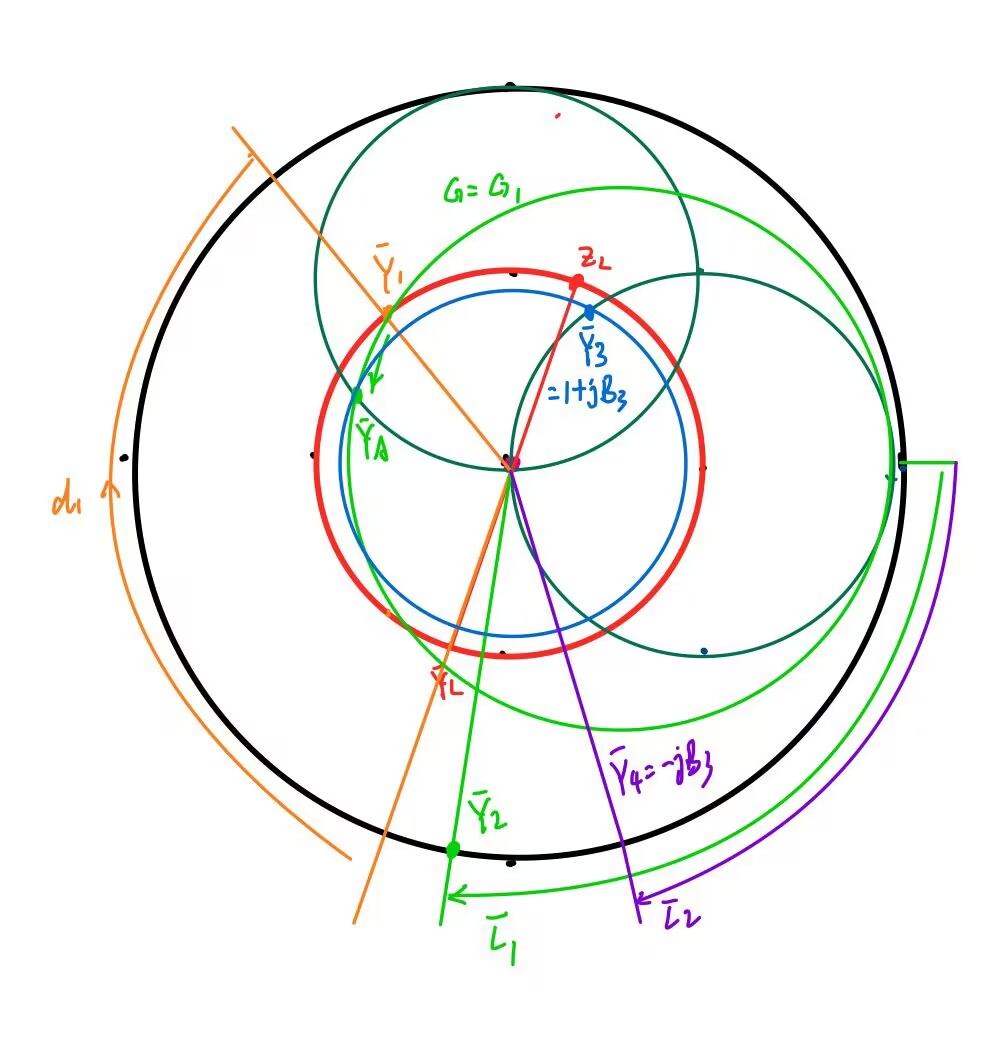
1. 把可匹配圆绕着单位圆的圆心旋转$$，画出辅助圆（深绿色）

2. 确定$$位置（鲜红色）

3. 从$$开始，沿其所在的等反射系数圆顺时针旋转$$，得到$$（橙色）

4. 因为$$是纯纳，所以$$和$$在一个等电导圆上。画出$$所在的等电导圆$$，这个等电导圆和辅助圆的交点就是$$。由$$计算出$$，绘制$$，读出$$的电标度，有（鲜绿色）： $$

5. 画出$$所在的等反射系数圆，交可匹配圆$$于$$点。读出$$.（蓝色）

6. 画出$$，有（紫色）： $$

双支节匹配过程

波导理论

导行波的传播特性

导行波的场量都有因子$$，其中$$。由麦克斯韦方程和边界条件推导（意思就是我也不想推导）可知： $$ 其中$$为电磁波在无限媒质中的波数，它由波的频率和传播介质决定。$$叫波导的截止波数，它由波导系统横截面的边界条件决定，这两个“波数”都是实数。于是，随着频率的不同，$$有以下三种情况：

• $$，此时有$$，因为场量不随着距离增长而衰减，称为传输状态。
• $$，此时有$$，此时场量随着距离增长而指数衰减，称为截止状态。
• $$，这个叫临界状态，分析时认为不属于传输状态，波不能传输。

既然有了“截止波数”$$的定义，我们也可以顺势定义出截止频率、截止波长：

• 截止频率$$ $$

• 截止波长$$ $$ 其中$$是理想介质^[1]中的光速。

于是，导波系统传输TE波或TM波的条件是： $$ 我们进一步分析传输状态时的导行波。理想导波系统中的相波长^[2]称为波导波长，记作$$。根据相波长和相位常数的定义，有： $$ 我们可以计算出，对于相位常数$$，有： $$ 于是，相波长为 $$ 根据相速度的一般公式$$，相速度为： $$ 根据群速度的一般公式$$，将$$中的$$用$$表示，有： $$ 以上就是会经常用到的一些传播特性参量。

导波模式

矩形波导

导通模式下矩形波导中TM波的通解为：

【一大坨式子，里面有两个参量$$和$$】

这里的$$和$$就是波导边界条件决定的正整数，称作波指数。$$表示沿着波导长边分布的半驻波个数，$$表示沿着波导短边分布的半驻波个数。$$和$$都不能是零。每一个$$都对应着一种电磁场分布，即一种波形，或者说，模式，记作$$

导通模式下矩形波导中TE波的通解为：

【一大坨式子，里面有两个参量$$和$$】

这里的$$和$$都是自然数，但是不能同时为零。每一个$$都对应着一种模式，记作$$

将各种$$和$$相互叠加，就能表示出矩形波导中所有可能存在的波形。那么怎么知道某种模式是否存在呢？我们有： $$ 也就是 $$ 考察波的$$(由频率和介质决定)，当满足传输条件$$或$$时，就存在对应的模式。观察这个式子，我们发现当$$对应相等时，TM波和TE波有着相同的截止波数，我们把这样的现象叫做模式简并^[3]。

通常，我们称截止波数最小（截止波长最大）的模式为主模，也叫基本模式或者最低模式。矩形波导的主模是$$模。

矩形波导的功率容量（最大传输功率）如下： $$ 其中$$是波导内媒质的击穿电压。

圆波导

圆波导的分析的大概形状和矩形波导是类似的，也有TE、TM波。

TM通解为：

【一大坨式子，里面有个参量$$】

其中$$表示第一类$$阶贝塞尔函数的第$$个零点。$$代表了一个TM波的模式，记作$$

TE通解为：

【一大坨式子，里面有个参量$$】

其中$$表示第一类$$阶贝塞尔函数的导数的第$$个零点。$$代表了一个TE波的模式，记作$$

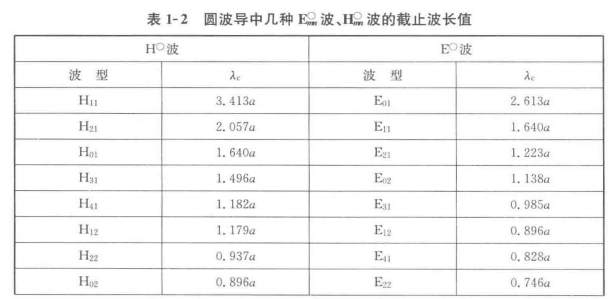
圆波导的截止波长一般查表给出。

截止波数表

在圆波导中，存在两种模式简并。第一种是E-H简并，因为对于第一类贝塞尔函数有$$，所以$$和$$的零点相等，因此$$和$$简并。第二种叫极化简并，是因为坐标$$的完全对称性引起的。在圆波导中，电磁场的横向分布存在着$$和$$两种形式，它们具有相同的截止波长，只是极化方向旋转90度。

---

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

1. 就是不导电的介质，不是自由空间。 ↩︎
2. 等相面在一个周期内移动的距离 ↩︎
3. 严格的定义是：模式简并：截止波数相同但是场分布不同的现象 ↩︎