关于离散系统和Z变换的那些事

离散系统和Z变换，与连续系统和Laplace变换很像，但也有些不同，可以对比学习。 本文合计5598字。

@[toc]

---

离散时间信号与系统

常用基本序列

1. 单位样值序列（对应冲激函数） $$\delta (n)=\{\begin{array}{ll}1& n=0\\ \\ 0& \text{others}\end{array}$$ 于是，仿照把任意信号分解成冲激函数和的形式，我们可以把任意序列分解成单位样值序列的和的形式，并且这个操作比在连续函数里更直观，即： $$x(n)=\sum _{m=-\mathrm{\infty }}^{\mathrm{\infty }}x(m)\delta (n-m)$$

2. 单位阶跃序列（对应单位阶跃函数） $$u(n)=\{\begin{array}{ll}1& n\ge 0\\ \\ 0& n<0\end{array}$$ 类似于单位冲激函数和单位阶跃函数的关系，有： $$u(n)=\sum _{m=-\mathrm{\infty }}^n\delta (m)$$ 和单位阶跃函数不同，$u(0)$有明确定义，为$1$.

3. 矩形序列

   矩形序列$$指的是从0开始（含0），含$$个$$的序列，即： $$ 矩形序列是两个单位阶跃序列的组合。有： $$

4. （单边）指数序列 $$ 当$$时收敛，$$和$$时发散。

   当$$时会在$$轴两侧摆动。

5. 正弦序列

   正弦序列是由正弦函数采样的序列，有： $$ 其中$$是采样周期。定义数字角频率： $$ 与正弦函数不同，正弦序列不一定是周期序列。当且仅当 $$ 是有理数时，正弦序列才是周期序列。

离散序列基本运算

一般的运算和连续信号（函数）没有多少区别。需要注意的是压扩运算。压扩运算需要去除某些点，或者补充某些0点。

离散时间系统

离散时间系统的描述和连续时间系统差别不大。不同于连续时间系统中常用积分器，离散时间系统中常用延时器，其符号为一个方框中写了一个“D”，作用是输入$$，输出$$。

记忆与无记忆、线性与非线性、时变与时不变、稳定与不稳定的含义和连续时间系统没有区别。

差分方程时域求解方法

离散时间系统的数学表达式常用差分方程来表示，一般差分方程的形式为： $$ 求解的过程和微分方程类似：首先将方程右边置0求得齐次解；然后根据激励信号的特点选取含待定系数的特解，代入方程求得特解；再将齐次解和特解相加得完全解；最后代入 初始条件 求待定系数。

1. 求齐次解

   将方程右边置0，得： $$ 特征方程为： $$ 这是一个关于$$的多项式方程。求解特征方程得到特征根$$。

   如果$$是单根或者共轭复根，那么齐次解中含有一项： $$ 如果$$是$$重根，那么齐次解中含有项： $$

2. 选取特解

   常见激励和它对应的特解如下：

   激励$$	特解	说明
   $$	$$	所有特征根不为1
   $$	$$	1是$$重特征根
   $$	$$	$$不是特征根
   $$	$$	$$是特征单根
   $$	$$	$$是$$重特征根
   $$或$$	$$ 或 $$	其中$$,$$不是特征根

【例】求解差分方程 $$ 其中激励为$$， 起始条件 为$$。

【解】特征方程为： $$ 特征根为 $$ 则齐次解为 $$ 由于$$，2不是特征根，选特解形式为 $$ 代入方程，有： $$ 两边同时除以$$，有： $$ 得特解： $$ 则完全解形式为： $$ 代入初始条件.因为方程右边的激励只在$$处有定义，我们要把已知的$$转换成$$.有： $$ 得： $$ 将上述条件代入完全解形式，得： $$ 于是可解得完全解： $$

零输入和零状态响应

1. 零输入响应

   零输入响应就是只考虑起始状态，而把输入置0时，系统的响应。也就是 $$ 的解。其中$$表示零输入（Zero Input）。

2. 零状态响应

   零状态响应的意思是起始状态全为0，仅仅考虑外加激励，所引起的响应。也就是 $$ 其中$$表示零状态（Zero State）。

可以通过零输入响应和零状态响应求和的办法求解全响应。

【例】求解差分方程 $$ 其中激励为$$，初始条件为$$。

【解】特征方程为： $$ 特征根为 $$ 则齐次解为 $$ 因为初始条件包含了激励信号的影响，因此需要求出起始条件为： $$ 则有： $$ 解得零输入响应为： $$ 然后求零状态响应。由于$$，2不是特征根，选特解形式为 $$ 代入方程，有： $$ 两边同时除以$$，有： $$ 得特解： $$ 则零状态响应的形式为： $$

因为求解的是零状态响应，因此此时系统的初始条件为：$$。代入差分方程，得初始条件： $$ 代入待定系数，解得： $$ 则全响应为 $$

单位样值响应

单位响应就是激励信号是$$时的零状态响应。它具有齐次解的形式，而且具有固定起始条件，即： $$

【例】求以下系统的单位样值响应 $$ 【解】先求系统 $$ 的单位样值响应$$，再由线性时不变特性求$$.

齐次解的形式为： $$ 代入固定起始条件$$： $$ 得： $$ 有： $$

卷积和

两个序列$$和$$的“卷积和”定义如下： $$ 卷积和具有交换律、结合律、分配律，此外，还有：

1. 移不变性 $$

2. 序列和单位样值序列的卷积 $$

3. 序列和单位阶跃序列的卷积 $$

在计算两个有限长度序列的卷积时，可以像列乘法竖式一样，先把两个序列右对齐，然后算“乘法”（只是不进位），即：

1. 两序列右对齐
2. 逐个样值对应相乘，不进位
3. 同列乘积相加

得到的结果$$的第一个数的下标是两个原始序列的第一个数的下标的和。

对于无穷长序列一般只能通过定义公式计算。

离散时间信号与系统变换域分析

$$变换

类似于拉普拉斯变换，Z变换也分为双边和单边。

双边$$变换的定义如下： $$ 单边$$变换的定义如下： $$

那么为什么和拉普拉斯变换这么像呢？这是因为$$变换可以从拉普拉斯变换导出。

考虑对一个连续时间信号$$进行时间间隔为$$的理想冲激抽样，抽样所得的信号记为$$，则有： $$ 对上式取$$变换，有： $$ 对调积分求和、利用冲激函数性质，有： $$ 设$$，由于$$是给定常数，则$$是$$的函数，则有： $$ 在一般的离散系统中，让$$，则有： $$ 一个序列的$$变换，实际上是一个系数为这个序列的样值，变量为$$的幂级数。即： $$

$$变换的收敛域

既然是从拉普拉斯变换导出来的，而且还是幂级数，那就不得不讨论收敛域。

复习一下，分析里面判断级数收敛有很多方法，其中最常用的有达朗贝尔判别法，即对于变号级数， $$ 如果$$，那么绝对收敛；如果$$，那么发散。

结合拉普拉斯变换，我们把序列分成左边序列，右边序列，双边序列来讨论。由于 $$ 我们可以通过下图的方法来建立S平面和Z平面的联系。

img

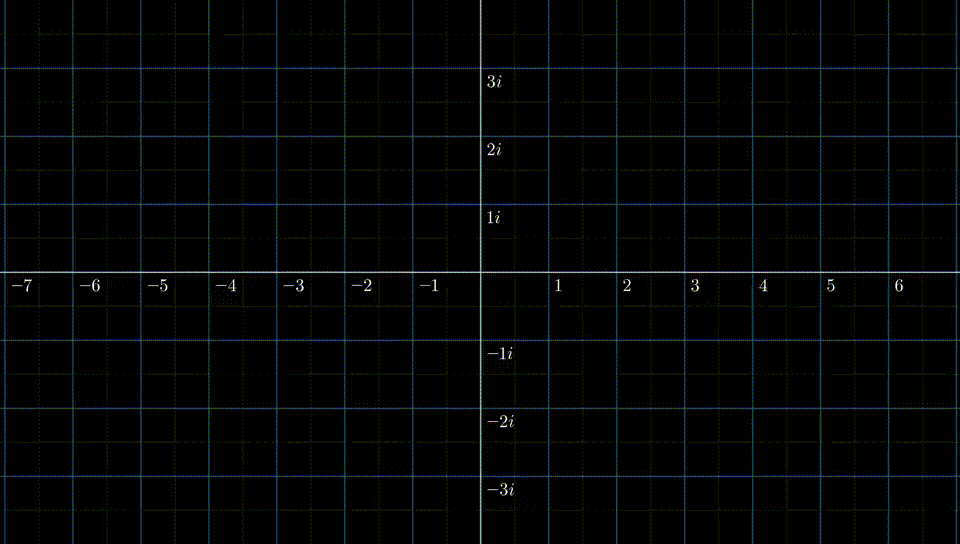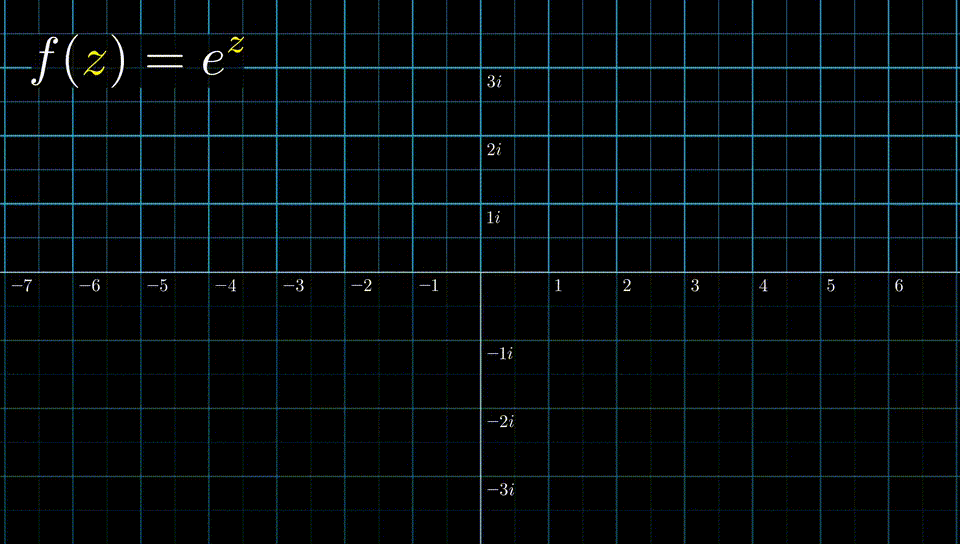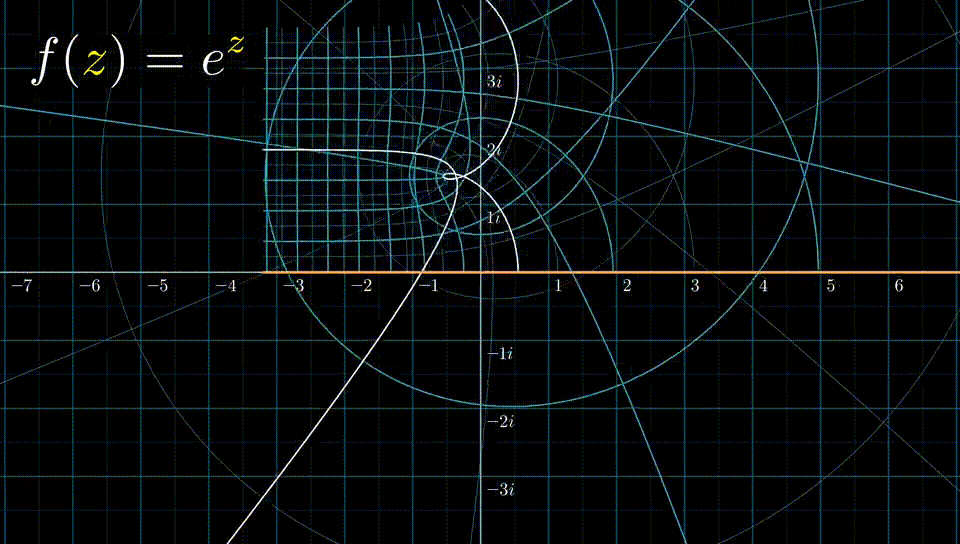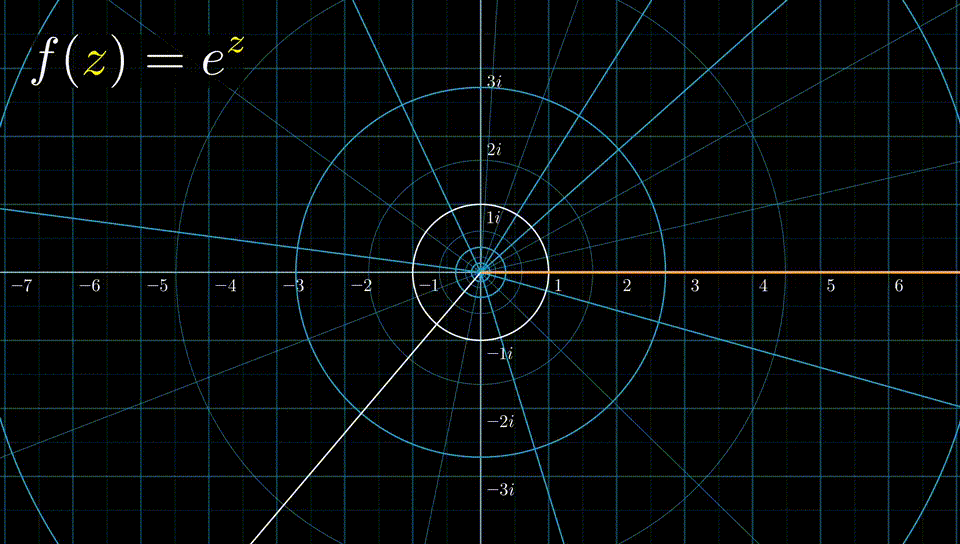
有：

序列（函数）类型	Z变换收敛性形状	拉普拉斯变换收敛域形状
右边	以原点为中心的圆之外 $$	右半平面 $$
左边	以原点为中心的圆之内 $$	左半平面 $$
两边	以原点为圆心的圆环 $$	条带 $$

对于有限长的序列，收敛域是除去零点和无穷远点的整个Z平面。

常见序列的$$变换

序列名称	序列表达式	$$变换	收敛域
单位样值序列	$$	$$	全平面
单位阶跃序列	$$	$$	$$
因果指数序列	$$	$$	$$

$$变换的性质

设 $$

时域性质

1. 反褶性质 $$

2. 扩展性质 $$

3. 位移性质

   1. 单边

      若$$是双边序列，有： $$ 则有： $$ 请注意这里的“位移”：$$和拉普拉斯变换里的“位移”$$，以及傅里叶变换里的“位移”$$的区别。

      特别的，如果$$是因果序列，那么有： $$

   2. 双边

      双边位移性质比较简单。 $$

4. 线性性质

频域性质

1. $$域微分-序列线性加权 $$

2. $$域压扩-序列指数加权 $$ 特殊的，如果要实现$$域反褶运算，有： $$

其它性质

1. 时域卷积 $$

2. 初值定理

   对于因果序列 $$

3. 终值定理 $$

利用$$变换性质求其它常用序列的$$变换

1. 单位样值序列的平移$$

   由时移性质，有： $$

2. 斜变序列$$

   由$$域微分-线性加权性质，有： $$

3. 因果余弦序列$$

   由欧拉公式： $$ 和已知的公式 $$ 结合线性性质，得 $$ 同理，因果正弦序列为： $$

逆$$变换的求解

一般的线性时不变系统的$$变换表达式往往具有有理多项式的形式。

长除法

长除法的意思就是根据$$变换的定义，直接求解幂级数的系数，从而求解原始序列。

当收敛域形式为$$时，幂级数表现出洛朗级数的形式，序列是右边序列，此时应把分母整理成降幂形式，再做长除法。

当收敛域形式为$$时，幂级数表现出泰勒级数的形式，序列是左边序列，此时应把分母整理成升幂形式，再做长除法。

这种长除法只能得到序列的部分样值，而且多用于单边$$变换。对于双边$$变换，一般用部分分式展开法。

部分分式分解法

部分分式分解法的核心思想是把有理多项式分式分解成基本分式 $$ 的和，然后由于 $$ 或者 $$ 来求解原始序列。

【例】求解： $$ 分收敛域为：(1) $$ (2) $$两种情况。

【解】首先对 $$ 进行分解，过程略，如果不会请参考拉普拉斯变换部分相关内容。有： $$ 则： $$

1. 收敛域为$$

   此时，有： $$

2. 收敛域为$$

   这时要考虑两个分式分别代表的收敛域是什么。因为线性组合的收敛域是各项的收敛域的交集。我们经分析，得：第一项对应收敛域$$，第二项对应收敛域$$。(如果反过来，那么收敛域就是空集，这和题目不符)，因此： $$

对于右边序列，如果出现共轭复根的情况，即 $$ 则有 $$ 可以使用mathematica验证上述推导，输入：

ZTransform[k*(Sqrt[a])^(n - 1)*Sin[n*Pi/2]*UnitStep[n], n, z]
MATHEMATICA

输出： $$ 对于2阶重极点，有： $$ 对于更高阶的极点，有： $$

用$$变换求解差分方程

一般差分方程的形式如下： $$ 对等式两边取$$变换： $$ 则系统全响应（的$$变换）为： $$ 其中第一项代表零状态响应，第二项代表零输入响应。

......麻了没？这么多分式，$$，我打着都麻。其实这玩意很简单的，下面通过一个例题给大家表演一下。

【例】差分方程 $$ 其中激励为$$， 起始条件 为$$。求零输入、零状态和全响应。

【解】对方程两边取$$变换，有： $$ 代入数据： $$ 则： $$ 其中第一项代表零状态响应，第二项代表零输入响应。有： $$

$$

则： $$ ($$)

离散系统传递函数

就是单位样值响应（零状态）$$的$$变换$$,一般有如下形式：

$$

其中$$就是零点，$$就是极点。对于因果序列而言，极点分布和$$大致时域形状的关系如下：

$$极点位置	$$时域形状
单位圆内实数	指数衰减序列
单位圆内共轭复数	衰减的正弦序列
单位圆外实数	指数增长序列
单位圆外共轭复数	增长的正弦序列
单位圆上实数	常序列（一阶）或逐渐增大
单位圆上共轭复数	幅度为常数或逐渐增大的正弦序列

由此可以看出极点分布和系统稳定性的关系。另外，这个表也可以由$$平面变换得出。

至于因果性，那就更简单了。只要系统函数的极点分布在$$平面内的一个半径有限的圆内就行，即保证收敛域为 $$

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：