关于傅里叶变换的那些事

所谓的变换，也就是信号的正交分解。如果两个函数的内积为$0$，我们称为这两个函数正交。那么对于任意信号$f(t)$，都可以写成一组正交函数系的和的形式（可以对比正交向量理解），这就是信号的正交分解。通过正交分解，可以对信号的特性有进一步的认识，也可以简化信号的分析和计算。

傅里叶级数

傅里叶级数是 周期信号 基于正交函数系$\{e^{j\omega t}\}$的正交分解。

三角函数形式的傅里叶级数

三角函数形式的傅里叶级数就是我们最熟悉的傅里叶级数。对于满足以下条件的函数$f(t)$:

• 周期函数，周期为$T_1$，角频率为${\omega }_1=2\pi /T_1$
• 间断点个数有限（可数）
• 极大极小值个数有限（可数）
• 绝对可积

有： $$ 其中$$叫直流分量，$$叫$$次谐波余弦分量，$$叫$$次谐波正弦分量。有计算公式： $$

$$

$$

当然，也可通过和差化积公式，转换成只有正弦或余弦分量的形式，此处不再赘述。

有： $$

指数形式傅里叶级数

因为： $$

$$

代入三角函数形式傅里叶级数中，就能得到指数形式傅里叶级数。这里给出部分关键步骤供参考。 $$ 其中 $$ 即 $$ 可以看出，$$一般而言是一个复数。它的模长和幅角满足： $$

$$

函数的对称性和傅里叶级数

因为$$是偶函数，$$是奇函数，所以函数本身的奇偶对称性和傅里叶系数的奇偶对称性有关系。

信号	$$	$$	$$	$$
奇函数	0	不为0	纯虚数	$$
偶函数	不为0	0	实数	$$
奇谐函数[1]	只含奇次谐波	只含奇次谐波	同前	同前
偶谐函数	只含直流分量和偶次谐波	同前	同前	同前

我们需要注意到：一个“偶谐函数”，和一个周期为$$的函数，实质上是一回事。

从傅里叶级数看傅里叶变换

傅里叶级数只能描述周期函数。但是我如果非得描述非周期函数，又会怎么样呢？我们来考虑一下怎么把非周期函数强行变成周期函数，其实只需要让周期$$趋向于无穷大就好了。

对于 $$ 让$$趋向于无穷大，则$$趋向于无穷小。因为函数满足绝对可积条件，所以右边是一个有限值比无穷大，趋向于0。而左边因为$$趋向于无穷小，取值点趋向于连续。有没有发现，这个过程有一点点像随机变量从连续型变成离散型时，分布列的变化情况（一方面，取值趋向于无穷小；另一方面，自变量趋向于连续）。于是，类似于“概率论”的知识，我们也可以定义“频谱密度函数”，让$$，有 $$ 这就是我们常说的傅里叶变换。

傅里叶变换

傅里叶变换的定义式

$$

基本信号及其傅里叶变换

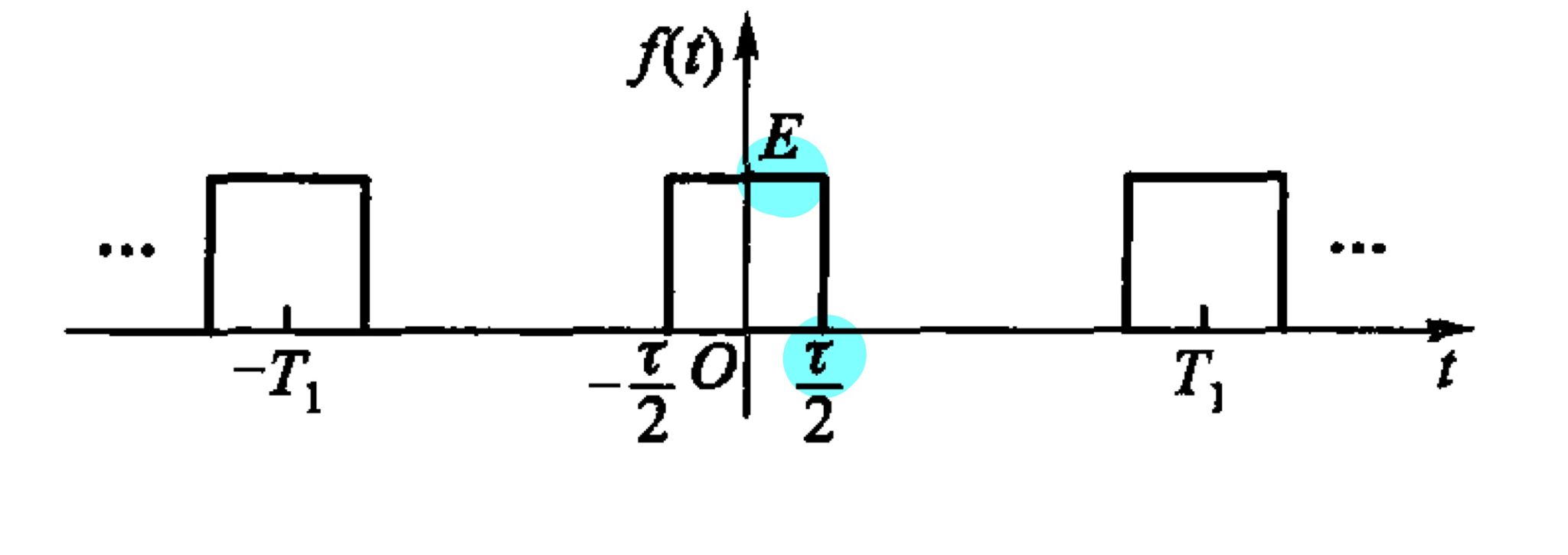
1. 矩形脉冲信号（门信号）

   即： $$ 有： $$

2. 单边指数信号 $$ 则 $$ 类似地， $$ 则 $$

3. “偶”双边指数信号

   把前面两个单边指数信号加起来就行了。 $$ 则 $$

4. 符号函数 $$ 为求符号函数的傅里叶变换，先求“奇双边指数函数”的傅里叶变换，然后让指数系数趋向于0即可。

   奇双边指数函数，即 $$

   $$

   

   image-20220627114355617

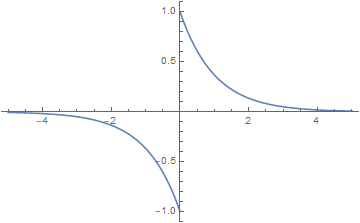
   当$$时，这个函数就趋向于$$。如图是$$的图像：

   

   image-20220627114553417

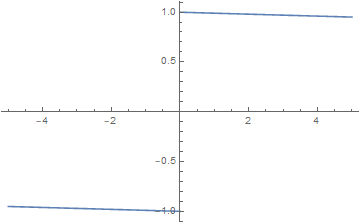
   则有： $$

5. 冲激信号 $$

6. 阶跃信号 $$ 这个结果可以通过符号函数平移得到。

傅里叶变换的性质

如果有： $$ 则有：

基于定义的性质

1. 对称性 $$

2. 奇虚偶实性

   • $$是偶函数
   • $$是奇函数
   • 如果$$是实偶函数，则$$是实偶函数
   • 如果$$是实奇函数，则$$是虚奇函数

基于时间运算的性质

1. 反褶性质 $$

2. 时移性质 $$ 可以说：时移不改变幅频特性，而改变相频特性。

3. 压扩性质 $$ 对于频域带限信号，时域的压缩和扩展，会导致频谱范围的增大和减小，频率分量的减少和增加。

4. 时域综合性质 $$

5. 线性

6. 时域微分性质 $$ 进一步： $$ 因为函数加上任意常数后，微分都相同。在运用这个性质时，要把信号的直流分量提取出来单独处理。例如：尝试利用时域微分性质和线性性质分别由$$函数的傅里叶变换计算$$的傅里叶变换，并比较结果。

7. 时域积分性质 $$

基于频域运算的性质

1. 频移性质 $$

2. 频域微分-时域线性加权性质 $$

卷积性质

1. 时域卷积 $$

2. 频域卷积 $$

由变换的性质计算常用信号的傅里叶变换

1. 直流信号$$

   由 $$ 因对称性，有： $$ 因线性，有： $$

2. $$

   由 $$ 因对称性，有： $$ 因线性，有： $$

3. 正余弦信号

   由 $$ 因频移性质，有： $$ 因三角函数分解公式： $$ 有： $$

4. 三角脉冲信号

   定义三角脉冲信号$$为形如下面的信号，计算傅里叶变换。

   

   img

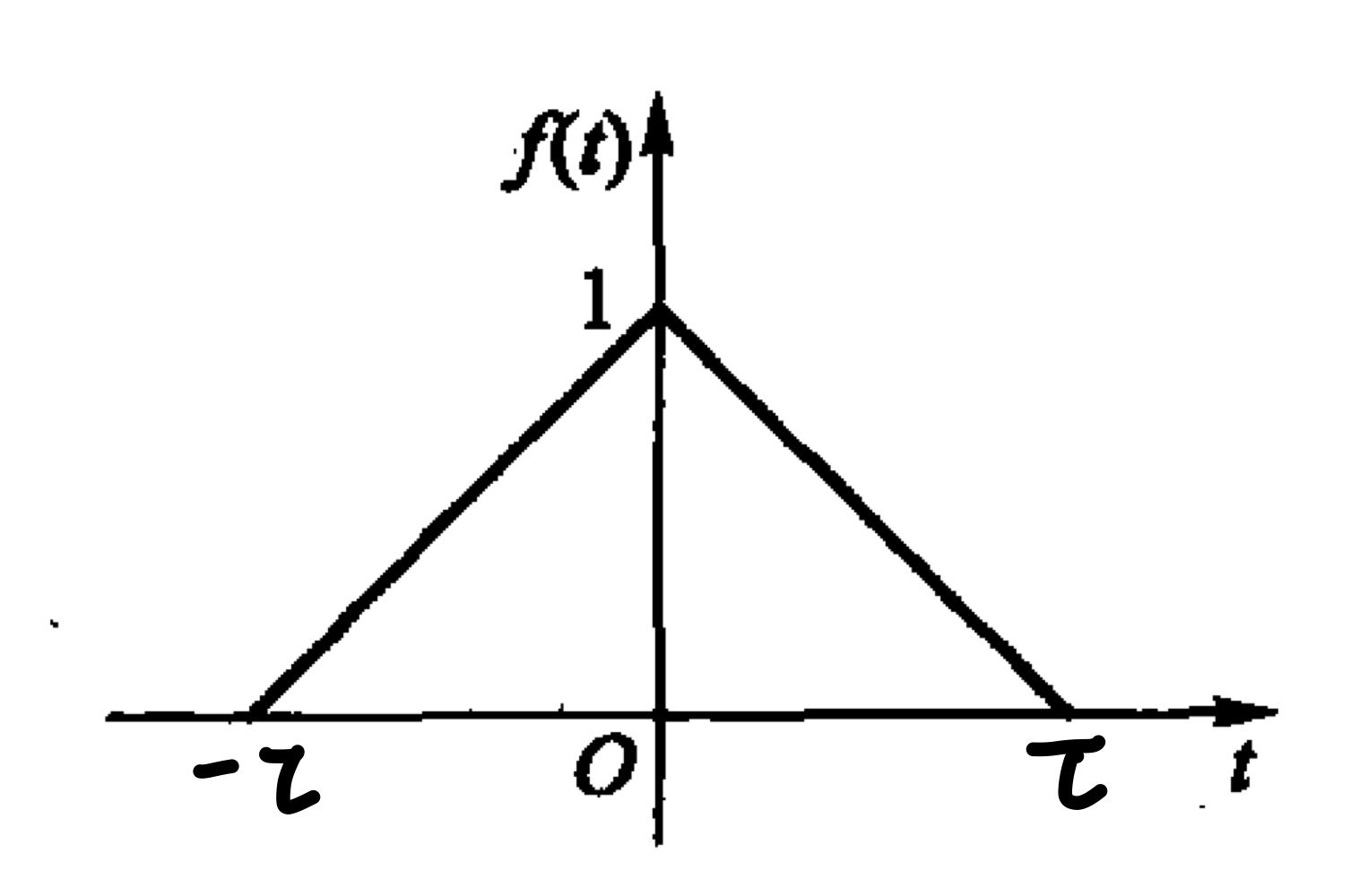
   由 $$ 则三角脉冲信号$$是门信号的卷积，具体地： $$ 由于 $$ 和卷积性质，有： $$

现将常用信号的傅里叶变换归纳如下：

这里提出一个趣味问题：

【例】：是否存在一个时域、频域都有限的信号？

【解】：不存在。如果时域有限，则信号可以表示为： $$ 而$$的傅里叶变换的频带是无限的。卷积之后，频带也是无限长的。频域有限情况同理可知。

周期信号的傅里叶变换

在之前，我们研究的是周期信号的傅里叶级数，和非周期信号的傅里叶变换。现在为了把它们都纳入傅里叶分析的框架中，我们要讨论周期信号的傅里叶变换。

我们都知道，周期信号的傅里叶系数$$叫“频谱函数”，而非周期信号的傅里叶变换$$叫“频谱密度函数”。那么如果我们非要用频谱密度函数来表示频谱函数，那么结果应该是出现在其角频率各次谐波处的冲激函数。（请联想概率论中，如果我们非要用“概率密度函数”来表示离散分布的“分布函数”，那么会出现什么现象？）

周期函数的傅里叶系数和它一个周期内函数的傅里叶变换的关系为：

$$

对于周期函数的傅里叶级数

$$

作傅里叶变换：

$$

由于频移性质：

$$

故：

$$

这就是一般周期信号的傅里叶变换。

典型周期信号的傅里叶变换

1. 正余弦信号

   正余弦信号的傅里叶变换我们之前已经求过了。现在我们可以从一个新的视角来考虑这个问题。对于余弦信号而言，有：

   $$

   则其傅里叶级数的系数为：

   $$

   则其傅里叶变换为：

   $$

2. 周期冲激信号

   周期冲激信号经常被用来采样，所以也算是一个常用的信号。我们来看一下它的傅里叶变换。

   周期冲激信号的定义是：

   $$

   其傅里叶系数为：

   $$

   则其傅里叶变换为：

   $$

   可以看出：周期冲激信号的傅里叶变换也是周期冲激信号。

3. 周期矩形脉冲信号

   周期矩形脉冲信号有两个参数：周期$$，脉宽$$，即：

   记作：$$，图中$$.

   在一个周期中，其傅里叶变换为：

   $$

   则周期矩形脉冲的傅里叶系数为

   $$

   故周期矩形脉冲的傅里叶变换为

   $$

抽样

一个基本的抽样过程等效于以下的模型：

img

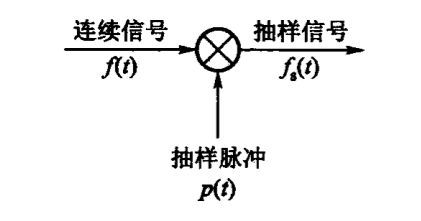
这里的"$$"是乘法的意思。即有：

$$

这里的$$就是脉冲信号，比如说周期冲激信号，周期矩形脉冲信号等等。

利用傅里叶变换的卷积定理，有（这里要熟练掌握冲激函数的卷积性质）：

$$

也就是说，抽样信号的频谱是连续信号频谱以$$为周期的周期延拓，并收到脉冲信号频谱$$和脉冲信号周期$$的加权。

于是，我们发现，如果要求不发生频域混叠，那么原始连续信号必须在频域是带限信号。但是这实际上是不可能存在的。但是信号的主要频域往往确实是有限的，其它部分的分量可以忽略不计，为此我们可以定义$$带宽，零点带宽等带宽（记作$$），把信号近似为一个频域带限信号。

那么，一个带限信号$$,如果其频谱存在在频域区间$$，则可用抽样值唯一表示$$,抽样值的间隔不能大于$$,其中$$，否则会发生频域混叠，这就是奈奎斯特采样定理。我们把$$称作“奈奎斯特频率”，这是不发生频域混叠的最小抽样频率。

为了从抽样信号中恢复出原始信号，对理想冲激抽样，我们用一个截止频率为$$，幅度增益为$$的零延时低通滤波器即可，其中$$满足$$.对于理想矩形脉冲抽样，滤波器的幅度增益应为$$

连续系统实频域分析

所谓的连续系统实频域分析，也就是利用傅里叶变换来分析连续系统。在本节，将首先介绍系统传递函数的概念，再介绍一类比较理想的系统：无失真系统，然后分析一类具体的系统：低通滤波器。

系统频率响应

定义系统单位冲激响应$$的傅里叶变换为系统频率响应。即：

$$

如果系统的激励为$$,激励的傅里叶变换为$$，那么对系统的响应的傅里叶变换，有：

$$

如果系统输入的是复指数信号$$，那么有：

$$

则有：

$$

这说明：系统对不同频率的正弦信号的幅度和相位加权不相同；不同的系统对相同频率的正弦信号的幅度和相位的加权也不相同。

对于频率响应$$，称$$为系统的幅频响应，而$$为系统的相频响应。

如果系统用微分方程

$$

可以直接写出其频率响应：

$$

在已知频率响应和激励，求系统响应时，一般有两种思路。其一是系统激励以傅里叶级数形式给出，这时只需要针对每个谐波分量计算对应的幅频响应和相频响应，然后把响应作用于激励即可。另一种思路是先求出激励的傅里叶变换，然后用图像和系统频率响应相乘，得到响应的傅里叶变换，最后得到结果。

无失真系统

输出响应能再现系统的输入，只有出现时刻和幅度不同，即没有改变输入波形的形状，这种系统叫做无失真系统。那么把冲激信号输入系统，就可以得到无失真系统的频响：

$$

则其幅频，相频特性如下：

$$

img

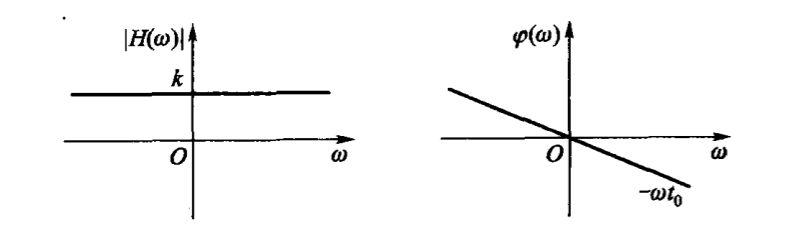
相频特性是一条直线的含义是：相频特性表示了系统的延时，对信号的所有频率分量，应该有相同的延时，即相位附加值相同。例如输入$$，那么理应得到输出$$，于是，为了对不同的频率分量得到相同的附加相移，就需要：

$$

低通滤波器

理想滤波器是在特定频段范围内的无失真传输系统。这里之所以只讨论低通滤波器，是其它滤波器可以由低通滤波器转换而来。具体如何转换，我们后面再说。

理想低通滤波器的频响特性如下：

$$

注意，切不可以以为理想低通滤波器的频响函数是频域门函数，因为还要考虑附加相移（时域延迟）。有：

$$

$$

对频响函数作傅里叶逆变换，可得单位冲激响应：

$$

img

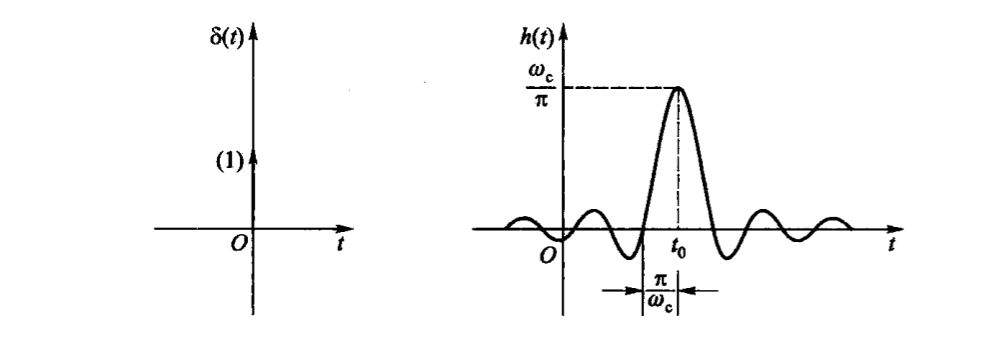
其它滤波器

• 高通滤波器

  无失真全通系统-低通滤波器=高通滤波器。因而，有：

  $$

  $$

• 带通滤波器

  带通滤波器可以由理想低通滤波器频响向两侧搬移，再对相频特性进行修正得到。

  $$

  $$

  其中

  $$

系统的因果性

我们都知道，$$系统因果的充要条件是：

$$

现在我们从频域考虑这个问题。

佩里维纳准则

一个幅频响应绝对可积的系统物理可实现的必要条件是：

$$

从直观角度考虑，佩里维纳准则要求系统的幅频响应不能衰减得太快。特别的，如果幅频响应在某个连续频带上为$$，那么系统就不可实现。

希尔伯特变换

接下来从时域入手，讨论判断系统因果性的充要条件。

从用卷积性质计算$$的傅里叶变换入手，设$$，那么$$构成一希尔伯特变换对。所谓的希尔伯特变换是指：

$$

把卷积展开，有：

$$

对一个系统作希尔伯特变换，实质上是将其经过一个$$相移器（注意：这里不是时移）。

希尔伯特变换将在《随机过程理论》中再次详细说明，这里只提两个重要性质：

• $$

• $$

则系统因果的充要条件是：频响函数$$的实部和虚部是一对希尔伯特变换对。

相关定理，以及能量和功率

为了动态地描述两个信号的相关关系，避免基于内积定义的相关系数所带来的种种漏洞.

对于能量信号，我们定义相关函数：

$$

定义自相关函数：

$$

如果信号是功率信号，上面的积分可能不收敛。定义功率信号的相关函数：

$$

自相关函数：

$$

在下学期学的《随机过程理论》中，我们将从期望的角度重新认识相关函数。

有“相关定理”：

$$

进一步，对自相关函数：

$$

联想到帕塞瓦尔定理：

$$

我们可以令$$为“能量密度函数”，也叫“能量谱函数”，它反映了能量在频域上的分布。则能量谱函数和能量信号自相关函数是一对傅里叶变换对。

对于功率信号，定义功率谱函数：

$$

则功率信号的功率谱函数和自相关函数也是一对傅里叶变换对，这叫做“维纳辛钦定理”。

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

1. 在一个周期里的两个半周期里呈现奇对称的函数，即(f(t)=-f(tT2))​ ↩︎