关于电磁场辐射的那些事

这部分主要讨论的是电磁波是如何产生的。

@[toc]

时变场的位函数

这一部分不是重点，我写完其它的再来写。

时变电偶极子的辐射

时变电偶极子

时变电偶极子是由大小相等、方向相反的两个点电荷组成的，其中按正弦形式变化。这两个点电荷间距为，电偶极子的有效长度（也叫电尺寸）为。有时，需要对电偶极子的电尺寸进行检验，看它是不是满足“远小于一”的条件。如果不满足，不应用电偶极子模型分析。

对于电偶极子之间的电流，有关系式：

写成复数形式，就是

全空间电磁场表达式

磁场：

电场

其中，有：

这个就是波阻抗。

时变电偶极子场的讨论

近区场

满足的条件，观察点离电偶极子比较近，这个区域称为近区。

在近区中，有：

而且

对于磁场，本来的表达式是：

中括号中第一项省去，后面的项省去，有：

同理，对于电场，有：

我们观察电场和磁场表达式，容易发现，近区场的主要成分是似静场，也就是近似于静电（磁）场的场。它的复坡印廷矢量是一个纯虚数，于是，这部分的能量不会被辐射出现，好像是被束缚在了近区，因此似静场也叫“束缚场”。我们可以说：时变电偶极子近区场的主要成分是束缚场；但是不可以说：近区场就是束缚场。

远区场

当时，观察点离电偶极子很远，这样的区域称为远区。

在远区中，有：

对于磁场，本来的表达式是：

中括号中的第二项省去，有：

很多同学可能不知道这个等号是怎么回事。我来说明一下：

有波长公式：

又有：

因此：

又因为：

因此：

可以看出，掌握电磁场中各个量的代换关系，是非常重要的。

同理，对于电场，有：

计算坡印廷矢量：

可以看出，在远区，电磁场有一个向外发射的功率流。远区中，电磁场携带的能量会全部辐射出去，因此远区场的 主要部分 ，也就是和成正比的这部分，被称为辐射场。辐射场中电场和磁场同相位，在等相位面上，电磁场振幅按照规律变化，因此辐射波是一个非均匀球面波。

必须说明的是：辐射场在近区也是存在的，不过十分微弱，不起主导作用。即：近区场也有能量发射的部分，远区场也有能量交换的部分，这里讨论的只是占主导作用的部分。因此 不能说：近区场就是束缚场，远区场就是辐射场 。随着的增长，辐射场（即反比于的项）比其它反比于高次方的项减少的慢，因此辐射场渐渐起了主导作用。用一个示意图描述，就是：

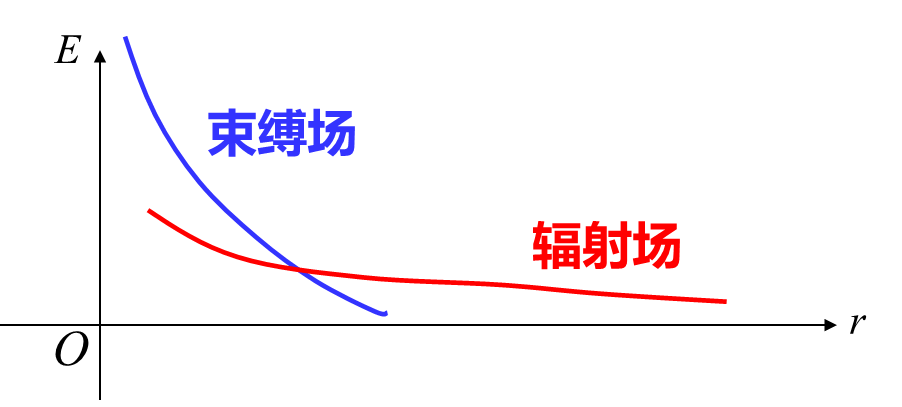
方向性函数

方向性函数的定义：

在时变电偶极子的情况下，有：

在Mathematica中运行代码：

1
2
SphericalPlot3D[
 Abs[Sin[\[Theta]]], {\[Theta], 0, Pi}, {\[Phi], 0, 2*Pi}]
MATHEMATICA

可以看出它长这样：

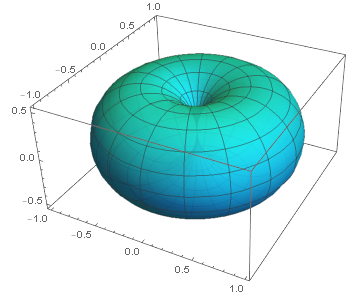
其E面方向图如下：

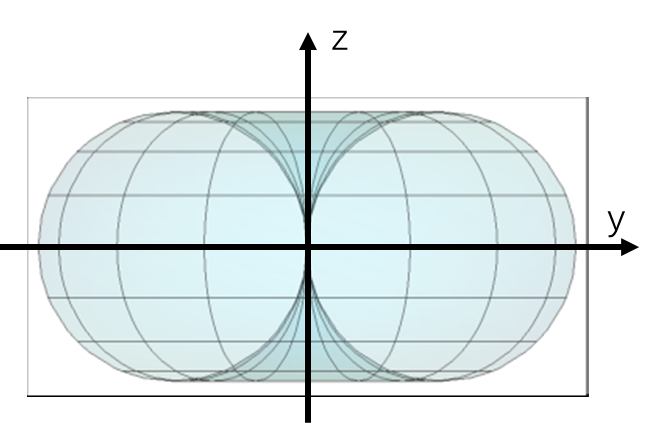
H面方向图如下：

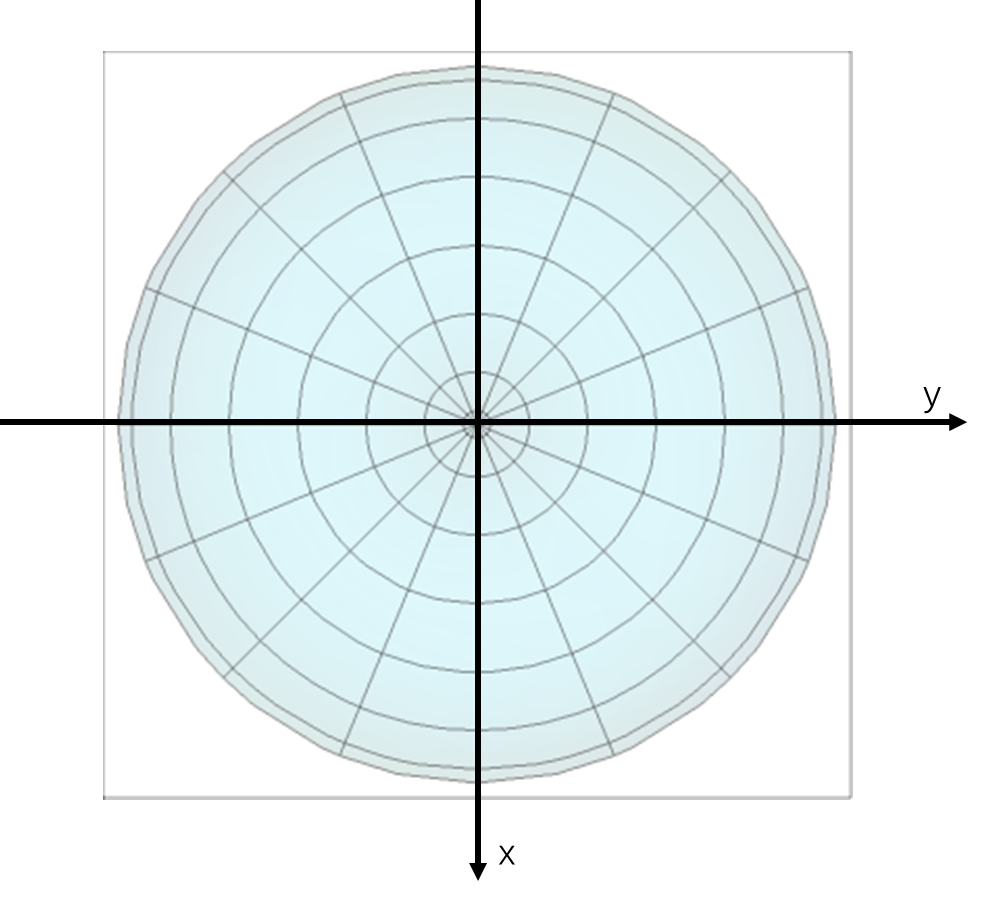
辐射功率和辐射电阻

时变电偶极子的辐射功率为：

由

得辐射电阻：

时变磁偶极子的辐射

时变磁偶极子

时变磁偶极子的模型是一个面积为，载有电流的导线环。当导线环的大小远远小于波长时，可以视为一个时变磁偶极子。

电磁对偶原理

在讨论时变磁偶极子之前，首先来介绍电磁对偶原理。在之前，曾经提到过对称形式场定律：

这两组方程形式完全相同，只是第一个式子的源是电流、电荷；而第二个式子的源是磁流，磁荷。因此，如果一个只含电流、电荷源的系统的解,已经求得，那么对于一个其它完全相同，只是把电流换成磁流，把电荷换成磁荷的新系统，它的解和，和应该有完全一样的形式

不妨对比一般性的两个系统a和b，如下。

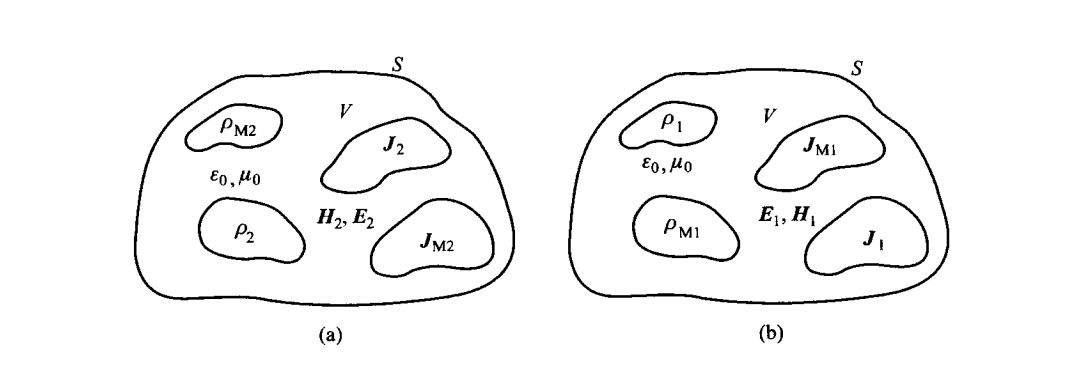
两个系统有完全相同的区域和边界，只是把电流和磁流，电荷和磁荷调换。那么存在以下的代换关系：

如果上面系统的解已经求出，按照上面的代换关系，就可以立刻得到系统的解。

全空间电磁场表达式

结合上面的电磁对偶关系，对于时变电偶极子式子里面的应该代换成,因此代换为,还有关系，可以直接写出全空间电磁场表达式：

时变磁偶极子场的讨论

近区场

近区场应该保留的最低次项（也就是的最高次项）,删去的指数项，有：

远区场

方向性函数

形状和电偶极子完全一样，但是E和H面的图要对换。

辐射功率和辐射电阻

由电磁对偶原理，有：

化简后， 有：

在自由空间中，把代入，有：

辐射电阻为：

其它天线简述

半波天线

可以理解为电偶极子天线长度变成半个波长。线天线的端点总是电流的波节点，中心点为波腹点。

方向性函数为：

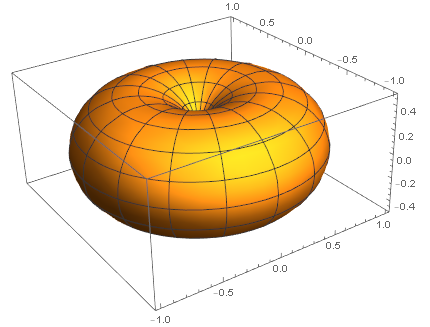
它的指向性比交变电偶极子更窄。

天线长度越大，方向函数的零、极点越多，主向越向轴线靠拢。

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：

笔记
#电磁场
关于电磁场辐射的那些事
https://suzumiyaakizuki.github.io/2022/06/21/关于电磁场辐射的那些事/
作者
SuzumiyaAkizuki
发布于
2022年6月21日
许可协议