关于拉普拉斯变换的那些事
拉普拉斯变换在许多工程技术和科学研究领域中有着广泛的应用，特别是在力学系统、电学系统、自动控制系统、可靠性系统以及随机服务系统等系统科学中都起着重要作用。本文大概写了一下常用的拉普拉斯变换技巧，非常的详细，我感觉任何人都能看懂。 本文约5200字，阅读时间22分钟。
拉普拉斯变换概述
说到拉普拉斯变换，就不得不提到奥列弗·赫维赛德。不得不说这位更是重量级，尽管大家可能不认识他，但是大家一定知道Heaviside()函数（在Mathematica中是HeavisideTheta[]函数）,这就是所谓的单位阶跃函数，我们一般简写为\(u(t)\)或者\(\varepsilon(t)\)。而且他在电子信息领域还有很多重要的贡献，比如说归纳整理了麦克斯韦方程组。而这里我们要说的是，他提出了运算微积分的思想，把常微分方程转换成了代数方程。具体地，他提出了微分算子\(p\): \[
p^n \leftrightarrow\frac{ {\mathbf d}^n()} { {\mathbf d}t^n}
\] 积分算子： \[
\frac{1} {p}\leftrightarrow \int_{-\infty}^t(){\mathbf d}\tau
\] 于是就能把常微分方程化成代数方程了。这种想法在当时并不被学界认可，但是我们现在发现这就是拉普拉斯变换的前身。
......扯远了，那么什么是拉普拉斯变换呢？我们都知道傅里叶变换很好用，但是要用它就必须得满足狄利特雷条件，其中有一条就是\(f(t)\)绝对可积，这可不是什么简单的条件，于是就导致很多常见的函数没有傅里叶变换。那么为了推广傅里叶变换，给\(f(t)\)乘上一个很强的衰减系数\(e^{-\sigma t}\),这时很多函数就变得绝对可积了。
容易发现，\(e^{-\sigma t}\)往往在\(t>0\)的时候才表现出”衰减“的性质，于是我们往往讨论单边拉普拉斯变换，即： \[ {\mathscr L}[f(t)]=F(s)=\int_{0-}^{\infty}f(t)e^{-(\sigma +j\omega)t} {\mathbf d}t \] 其中\(s={\sigma + j\omega}\).
拉普拉斯变换需要讨论收敛域的问题。我们把让上述无穷积分收敛的\(s\)所在的区域称为收敛域。收敛域的边界是平行于虚轴的直线。对于右边信号而言，收敛域往往是\(Re[s]>\alpha\)的形式，也就是右半边平面。在讨论右边信号和单边拉普拉斯变换时，往往省去对收敛域的讨论。但对于双边拉普拉斯变换来说，一定要讨论收敛域。因为此时对于同一个\(F(s)\)，不同的收敛域会导致反变换的结果不同。
拉普拉斯变换性质
设\({\mathscr L}[f(t)]=F(s)\)，则
拉普拉斯变换常用的性质有：
时域性质
时移性质： \[ {\mathscr L}[f(t-t_0)u(t-t_0)]=F(s)e^{-st_0} \] 需要注意到：\(f(t-t_0)u(t-t_0)\)、\(f(t-t_0)u(t)\)、\(f(t-t_0)\)是互不相同的。
压扩(相似)性质： \[ {\mathscr L}[f(at)]=\frac{1} {a}F(\frac{s} {a}) \]
线性性质
时域微分性质： \[ \begin{aligned} {\mathscr L}[\frac{ {\mathbf d}^n f(t)} { {\mathbf d}t}]&=s^nF(s)-s^{n-1}f(0_-)-s^{n-2}f'(0_-)-\cdots-f^{(n-1)}(0_-)\\\\ &=s^nF(s)-\sum_{k=0}^{n-1}s^{n-1-k}f^{(k)}(0_-) \end{aligned} \]
如果\(f(t)\)为因果信号，即\(f(t)=f(t)u(t)\)，那么： \[ {\mathscr L}[\frac{ {\mathbf d}^n f(t)} { {\mathbf d}t}]=s^nF(s) \] 我们看出这个形式和前面所说的”微分算子“有异曲同工之妙。这也是用拉普拉斯变换解微分方程的基础。
时域积分性质： \[ {\mathscr L}[\int_{-\infty}^tf(\tau){\mathbf d}\tau]=\frac{F(s)} {s}+\frac{f^{(-1)}(0_-)} {s} \]
频域性质
频移性质： \[ {\mathscr L}[e^{s_0t}f(t)]=F(s-s_0) \] 请注意和时移性质之间的区别。时间变成\(t-t_0\)，乘的指数因子也是\(e^{-st_0}\)，但是频域变成\(s-s_0\)后，乘的指数因子却是\(e^{s_0t}\)，符号不同。
频域微分性质： \[ {\mathscr L}[-tf(t)]=\frac{ {\mathbf d}F(s)} { {\mathbf d}s} \] 同样，注意符号。一般的，有： \[ {\mathscr L}[(-t)^nf(t)]=\frac{ {\mathbf d}^nF} { {\mathbf d}s^n} \]
频域积分性质： \[ {\mathscr L}[\frac{f(t)} {t}]=\int_s^\infty F(\lambda){\mathbf d}\lambda \]
其它定理
对于卷积运算，有卷积性质：
- 时域卷积
\[ {\mathscr L}[f_1(t)\bigotimes f_2(t)]=F_1(s)F_2(s) \]
- 频域卷积 \[ {\mathscr L}[f_1(t)f_2(t)]=\frac{1} {2\pi j}F_1(s)\bigotimes F_2(s) \] 频域卷积很少用到。
此外，还有终、初值定理：
初值定理 \[ f(0_+)=\lim_{s\to \infty}sF(s) \]
终值定理 \[ \lim_{t\to \infty}f(t)=\lim_{s\to 0}sF(s) \]
常用拉普拉斯变换表
| 原函数 | 像函数 |
|---|---|
| \(1\)或\(u(t)\) | \(\frac{1} {s}\) |
就一个？没错。因为其它的常用的基本上都能用性质推导出来。
\(t^n\)
由频域微分性质\({\mathscr L}[(-t)^nf(t)]=\frac{ {\mathbf d}^nF} { {\mathbf d}s^n}\)，将\(f(t)=u(t),F=s^{-1}\)代入，可得： \[ {\mathscr L}[t^n]=\frac{n!} {s^{n+1} } \]
\(e^{at}\)
由频移性质\({\mathscr L}[e^{s_0t}f(t)]=F(s-s_0)\)可得： \[ {\mathscr L}[e^{at}]=\frac{1} {s-a} \]
\(t^ne^{at}\)
对\(t^n\)的拉普拉斯变换应用频移性质，有： \[ {\mathscr L}[t^n e^{at}]=\frac{n!} {(s-a)^{n+1} } \]
\(\cos (\omega t)\)
由 \[ \cos(\omega t)=\frac{1} {2}(e^{-j\omega t}+e^{j\omega t}) \] 运用\(e^{at}\)的拉普拉斯变换，可得 \[ {\mathscr L}[\cos (\omega t)]=\frac{s} {s^2+\omega ^2} \]
\(\sin (\omega t)\)
由 \[ \sin(\omega t)=\frac{1} {2j}(e^{j\omega t}-e^{-j\omega t}) \] 得 \[ {\mathscr L}[\sin(\omega t)]=\frac{\omega} {s^2+\omega ^2} \]
虽说如此，表格还是需要的。现归纳如下：
| 原函数 | 像函数 |
|---|---|
| \(u(t)\) | \(\frac 1s\) |
| \(t\) | \(\frac{1} {s^2}\) |
| \(t^n\) | \(\frac{n!} {s^{n+1} }\) |
| \(e^{at}\) | \(\frac{1} {s-a}\) |
| \(te^{at}\) | \(\frac{1} {(s-a)^2}\) |
| \(t^ne^{at}\) | \(\frac{n!} {(s-a)^{n+1} }\) |
| \(\sin (\omega t)\) | \(\frac{\omega} {s^2+\omega^2}\) |
| \(\cos (\omega t)\) | \(\frac{s} {s^2+\omega^2}\) |
多项式分式的拉普拉斯逆变换
一个有理真分式形式的拉普拉斯变换式可以写成： \[ F(s)=\frac{N(s)} {D(s)} \] 其中\(N\)和\(D\)都是多项式，\(D\)的次数更高。接下来讲解如何计算这样的式子的拉普拉斯反变换。
基于代数方程的理论，上面的式子可以写成： \[ F(s)=\frac{K_1} {(s-p_1)}+\frac{K_1} {(s-p_1)}+\cdots+\frac{K_n} {(s-p_n)} \] 即分解成很多小分式的和，其中\(p\)为\(D\)的根。多项式的根可能有单根、多重根，共轭复数根三种情况，我们来分别讨论。
单根
单根对应的小分式为： \[ \frac{K_i} {s-p_i} \] 在计算时，只需要给\(F(s)\)两边同时乘以\((s-p_i)\)，这样就能把这个极点消掉了，然后将\(s=p_i\)代入\((s-p_i)F(s)\)中（温馨提示：不要看到\((s-p_i)\)乘以什么什么的形式就以为是0哦！），就能算出\(K_i\)了。
这个小分式对应的原函数是\(K_ie^{p_it}\).
举例如下：
【例】计算下式的拉普拉斯反变换 \[ \frac{2s^2+3s+3} {s^3+6s^2+11s+6} \] 【解】首先计算极点。打开计算器，按顺序输入：设置 8 2 3，进入求解三次多项式方程的页面。输入1 = 6 = 1 1 = 6，将分母的多项式输入计算器。按=，即可得到三个根为： \[ -3,-1,-2 \] 于是\(F(s)\)可以写为： \[ \begin{aligned} F(s)&=\frac{2s^2+3s+3} {(s+1)(s+2)(s+3)}\\ &=\frac{K_1} {s+1}+\frac{K_2} {s+2}+\frac{K_3} {s+3} \end{aligned} \] 我们看到都是单根，于是继续进行求解。
按计算器设置 1返回计算模式。依次在键盘上输入- 1 STO (-)[即A]，屏幕上显示
2-1 -> A
-1意思是给变量A赋值为-1.
按AC，在计算器上输入\((s+1)F(s)\)，即： \[ \frac{2A^2+3A+3} {(A+2)(A+3)} \] 按=,屏幕上的结果即为\(K_1=1\)
如法炮制，可以计算出\(K_2=-5,K_3=6\)
则原函数为 \[ f(t)=(e^{-t}+5e^{-2t}+6e^{-3t})u(t) \]
共轭复根
共轭复根对应的小分式为： \[ \frac{K_1} {s-(a+bj)}+\frac{K_2} {s-(a-bj)} \] 其中\(K_1\)和\(K_2\)是一对共轭复数。因为共轭复根归根结底也是单根，所以可以继续使用上面的解法来求解\(K_1,K_2\)，但是只用求解其中的一个就行，因为它们共轭。假设\((a+bj)\)对应的系数\(K_1=r\angle \theta=re^{i\theta}\),这对共轭复根对应的原函数为： \[ \begin{aligned} f(t)&=re^{j\theta}e^{(a+bj)t}+re^{-j\theta}e^{(a-bj)t}\\ &=re^{at}(e^{j(bt+\theta)}+e^{-j(bt+\theta)})\\ &=2re^{at}\cos(bt+\theta) \end{aligned} \]
【例】求解下式的拉普拉斯反变换： \[ \frac{2s+4} {s^2+2s+2} \] 【解】按照上题的办法用计算器求解极点，得极点： \[ -1+j,-1-j \] 于是原式可以写为： \[ \begin{aligned} F(s)&=\frac{2s+4} {[s-(-1+j)][s-(-1-j)]}\\ &=\frac{K_1} {s-(-1+j)}+\frac{K_2} {s-(-1-j)} \end{aligned} \] 下面求\(K_1\).按设置 2进入复数计算模式，按- 1 + ENG 输入\(-1+j\)，按STO (-)存入变量A中。输入 \[ \frac{2A+4} {A-(-1-j)} \] 按=,屏幕上显示计算结果为\(K_1=1-j\).
按shift 设置 ↓ 2 2将复数显示切换为模长-幅角形式，屏幕上显示：\(\sqrt{2}\angle -45\) ,这里的单位是度。按shift 设置 2 2把角度单位改为弧度，屏幕上显示\(\sqrt{2}\angle -\frac{1} {4}\pi\).
那么对应的原函数为 \[ f(t)=2\sqrt{2}e^{-t}\cos(t-\frac{\pi} {4})u(t) \]
多重根
\(k\)重根对应的小分式如下： \[ G(s)=\frac{K_1} {(s-p)^k}+\frac{K_2} {(s-p)^{k-1} }+\cdots+\frac{K_k} {s-p} \] 给两边同时乘以\((s-p)^k\)，有： \[ (s-p)^kG(s)=K_1+K_2(s-p)+\cdots +K_k(s-p)^{k-1} \] 于是我们知道： \[ K_m=\frac{1} {(m-1)!}\frac{d^{m-1} } {ds^{m-1} }[(s-p)^kG(s)]_{s=p} \] 这项对应的原函数为： \[ e^{pt}\left[\frac{K_1} {(k-1)!}t^{k-1}+\frac{K_2} {(k-2)!}t^{k-2}+\cdots+K_k\right] \]
【例】求解下式的拉普拉斯反变换： \[ \frac{s^2} {(s+2)(s+1)^2} \] 【解】因为题目已经帮我们因式分解好了，于是我们直接拆开： \[ F(s)=\frac{K_0} {s+2}+\frac{K_1} {(s+1)^2}+\frac{K_2} {s+1} \] \(K_0\)很容易计算，为\(4\)。
对等式两端同时乘以\((s+1)^2\)，有： \[ \frac{s^2} {s+2}=K_0\frac{(s+1)^2} {s+2}+K_1+(s+1)K_2 \] 将\(s=-1\)代入得\(K_1=1\)
在计算器中输入： \[ \left. \frac{ {\mathbf d} } { {\mathbf d}x}\left(\frac{x^2} {x+2}\right) \right |_{x=-1} \] 按等号，得\(K_2=-3\).
于是原函数为 \[ f(t)=(4e^{-2t}-3e^{-t}+te^{-t})u(t) \]
运算电路
运算电路说的就是在RLC电路中，通过把元件的时域\(u-i\)微分方程通过拉普拉斯变换转换成代数方程然后求解的过程，其操作过程和相量法是相似的。具体来说：
电阻
形式不变，仍为\(R\)
电容
如果电容的值为\(C\)，初值条件为\(u_c(0_-)\)，那么在运算电路中，电容模型变为\(\frac{1} {sC}\)，并且串联一个和初值电压方向相同，值为\(\frac{1} {s}u_c(0_-)\)的电压源。
电感
如果电感的值为\(L\)，初值条件为\(i_L(0_-)\)，那么在运算电路中，电感模型变为\(Ls\)，并且并联一个和初值电流方向相同的，值为\(\frac{1} {s}i_L(0_-)\)的电流源。
系统函数与响应的分解
在拉普拉斯变换下，系统函数有两种定义。
基于单位冲激响应的定义： \[ H(s)={\mathscr L}[h(t)]=\int_{0-}^{\infty}h(t)e^{-st} {\mathbf d}t \]
基于一般激励的零状态响应的拉普拉斯变换\(R(s)\)和激励的拉普拉斯变换\(E(s)\)的比值的定义： \[ H(s)=\frac{R(s)} {E(s)} \]
在之前的学习中，我们学过响应可以分为自由响应、强迫响应、暂态响应、稳态响应等部分，我们可以以拉普拉斯变换的视角来重新看待这些概念。
假设系统函数和输入激励只含一阶零极点，即： \[ H(s)=\frac{N(s)} {D(s)}=k_h\frac{\prod_{j=1}^m (s-z_j)} {\prod _{i=1}^n (s-p_i)} \]
\[ E(s)=k_e\frac{\prod_{l=1}^u(s-z_l)} {\prod _{k=1}^v(s-p_k)} \]
于是系统响应的拉普拉斯变换\(R=E\times H\)为： \[ R(s)=k_hk_e\frac{\prod_{j=1}^m (s-z_j)} {\prod _{i=1}^n (s-p_i)}\frac{\prod_{l=1}^u(s-z_l)} {\prod _{k=1}^v(s-p_k)} \] 拉普拉斯逆变换，得系统的响应\(r(t)={\mathscr L}^{-1}[R(s)]\)为： \[ r(t)=\left(\sum_{i=1}^nA_ie^{p_it}+\sum_{k=1}^vA_ke^{p_kt}\right)u(t) \]
自由响应和强迫响应
我们可以看到，左边的求和式\(\sum_{i=1}^nA_ie^{p_it}\)来自于\(H(s)\)，是系统本身（的极点）决定的，对应于微分方程的齐次解。我们知道 齐次解和激励无关，所以称之为自由响应。 而\(\sum_{k=1}^vA_ke^{p_kt}\)项来自于\(R(s)\)，也就是微分方程的特解。我们知道 特解取决于外加激励，所以称之为强迫响应。
暂态响应和稳态响应
我们将\(R(s)\)的极点分成位于“左半平面”和“虚轴以及右半平面”的两类。位于左半平面的极点带来的响应会乘以一个\(e^{-at}\)的系数（其中\(a>0\))，因此如果时间比较长，便会近似等于\(0\)。 这种左半平面的极点对应的响应是暂时的，因此称作暂态响应。 相反，位于虚轴或右半平面的极点带来的响应往往要不是\(\cos\)震荡形式，要不会乘以一个\(e^{at}\)的系数（其中\(a>0\)),这种响应 不会随着时间推移而消失，所以称为稳态响应。
系统框图
在之前的推文中其实我介绍了一种绘制系统框图的技术。现在我们来介绍一种基于拉普拉斯变换的，更简单的技术。
对于微分方程系统（\(n>m\)） \[ C_0r^{(n)}(t)+C_1r^{(n-1)}(t)+\cdots+C_nr(t)=E_0e^{(m)}(t)+E_1e^{(m-1)}(t)+\cdots+E_me(t) \] 有系统函数 \[ H(s)=\frac{\sum_{j=0}^mE_js^{m-j} } {\sum_{i=0}^nC_is^{n-i} } \] 因为我们系统框图里面一般都用积分器，所以我们也把系统函数进行一个变形（上下同除以\(s^n\)）也就是把微分方程变成积分方程（方程两边进行\(n\)次积分）： \[ H(s)=\frac{\sum_{j=0}^mE_js^{-n+m-j} } {\sum_{i=0}^nC_is^{-i} } \] 这样的系统可以拆分成两个系统的级联,设置中间变量\(W(s)\)： \[ H_1(s)=\frac{W(s)} {E(s)}=\frac 1 {\sum_{i=0}^nC_is^{-i} }\\ H_2(s)=\frac{R(s)} {W(s)}=\sum_{j=0}^mE_js^{-n+m-j} \] 经过变形， 有： \[ C_0W(s)=E(s)-W(s)\sum_{i=1}^nC_is^{-i}\\ R(s)=W(s)H_2(s) \] 于是框图如下所示：
系统幅相频特性和波特图
系统幅相频特性就是系统的响应随着输入信号频率的变化而变化的性质，而我们常用波特图来进行描述。波特图是一种比较特殊的绘图方式，其纵轴为\(20\lg H/\text{dB}\)，横轴为\(\omega\)，且横轴是对数坐标。（由于纵轴的\(\text{dB}\)已经隐含了对数坐标的事实，所以其实是双对数图）
一般来说，线性时不变系统的传递函数可以写作： \[ H(s)=H_0\frac{\prod_{j=1}^m (s-z_j)} {\prod _{i=1}^n (s-p_i)} \] 其中\(\{z_1,z_2,\cdots,z_m\}\)叫做系统的零点，\(\{p_1,p_2,\cdots,p_n\}\)叫做系统的极点。如果一个系统稳定，那么其极点一定在左半平面，而且极点个数一定大于等于零点个数。
用\(j\omega\)代替上面的\(s\)，有： \[ H(j\omega)=H_0\frac{(j\omega-z_1)(j\omega-z_2)\cdots(j\omega-z_m)} {(j\omega-p_1)(j\omega-p_2)\cdots(j\omega-p_n)} \] 取对数，因为对数可以把乘除式化为加减式，有幅频特性表达式： \[ \begin{aligned} 20\lg H(\omega)&=20\lg H_0\\ &+\left(20\lg \sqrt{\omega^2+z_1^2}+20\lg \sqrt{\omega^2+z_2^2}+\cdots+20\lg \sqrt{\omega^2+z_m^2}\right)\\ &-\left(20\lg \sqrt{\omega^2+p_1^2}+20\lg \sqrt{\omega^2+p_2^2}+\cdots+20\lg \sqrt{\omega^2+p_n^2}\right) \end{aligned} \] 由于复数作积是相角相加，复数作商是相角相减，有相频表达式： \[ \varphi(\omega)=\tan^{-1}\left(-\frac\omega {z_1}\right )+\tan^{-1}\left(-\frac\omega {z_2}\right )+\cdots-\tan^{-1}\left(-\frac\omega {p_1}\right )-\cdots \] 为表达方便，记： \[ \omega_z=-z,\omega_p=-p \]
幅频波特图
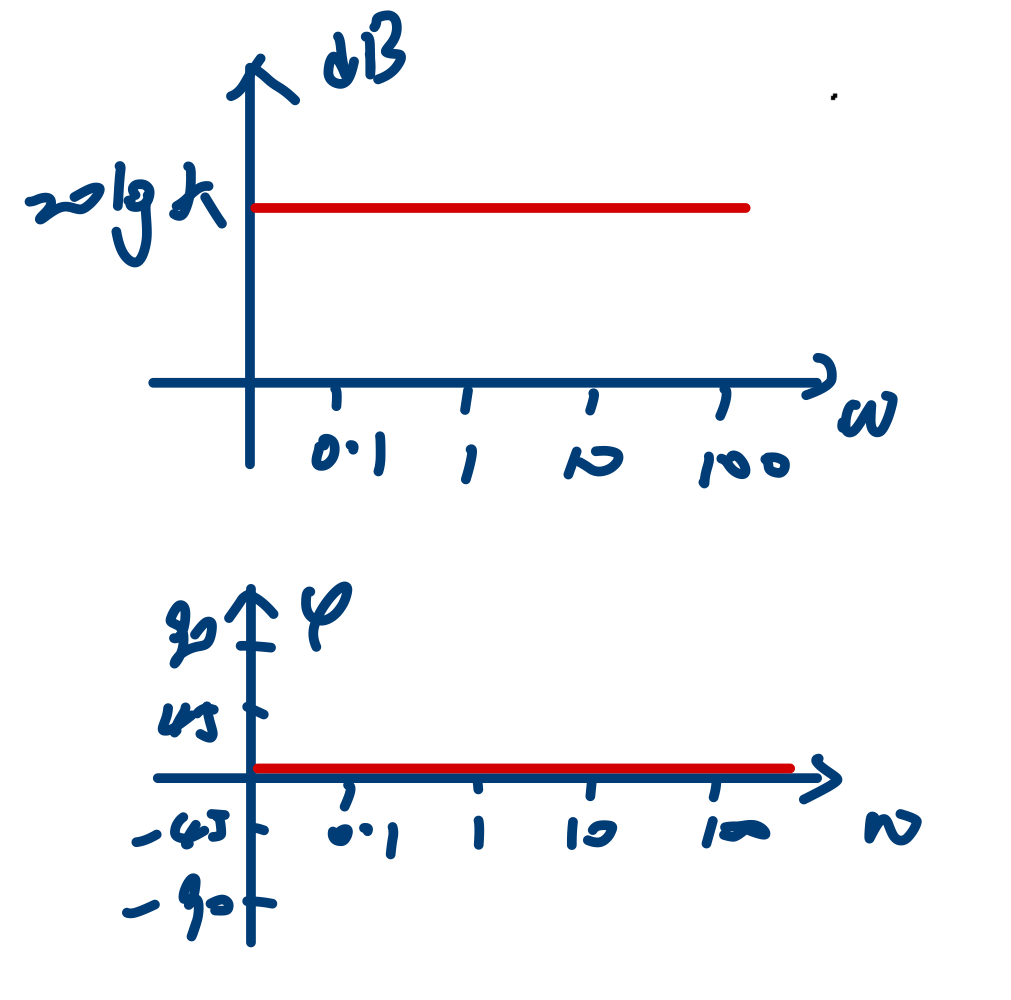
常数因子
即\(H'(\omega)=K\)项，有：
\(20\lg H'(\omega)=20\lg K\)是常数
\(\varphi(\omega)=0\)恒为0
对应的图像如下：
\(j\omega\)因子（零零点因子）
即\(H'(\omega)=j\omega\)，有：
\(20\lg H'(\omega)=20\lg \omega\)
\(\varphi(\omega)=90\degree\)
对应的图像如下：
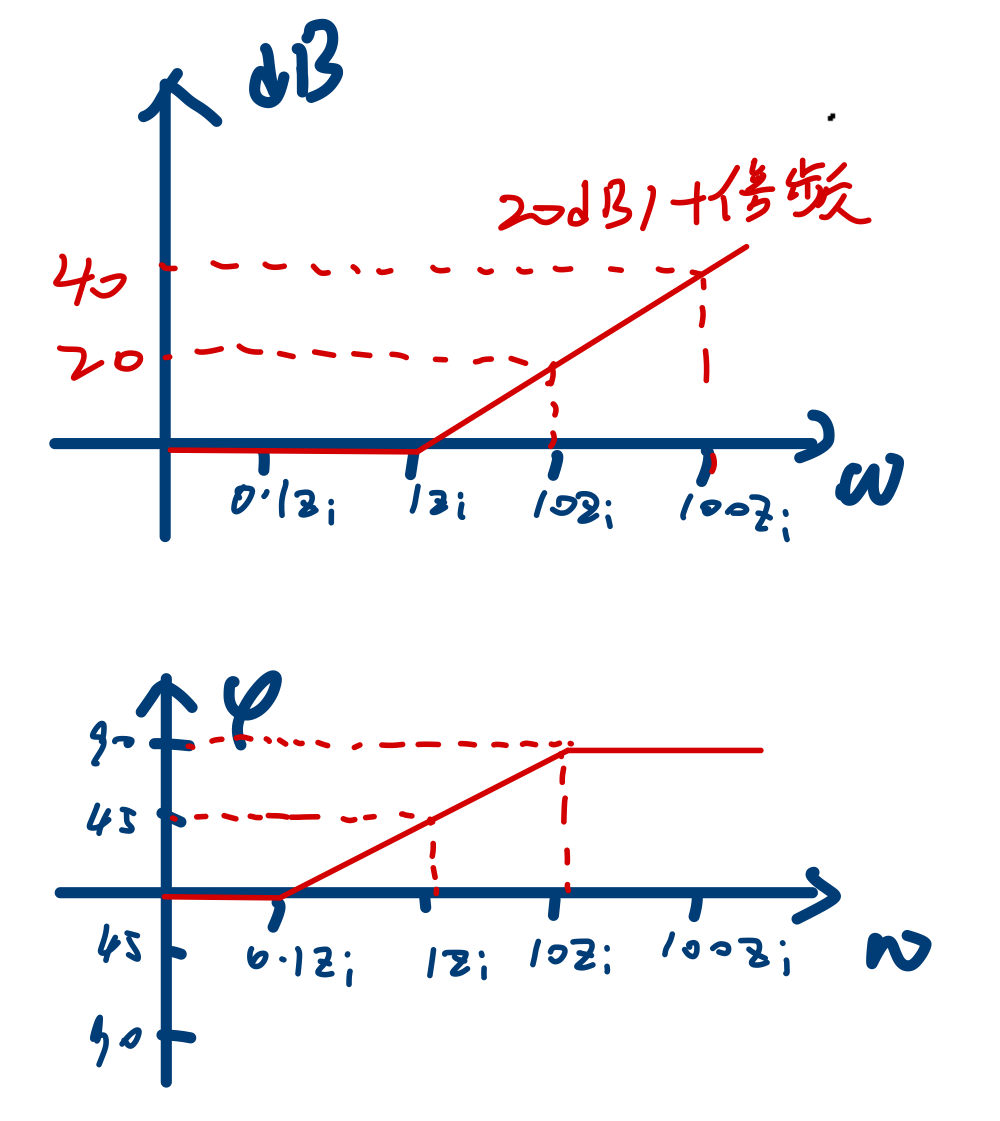
一般一阶零点因子
即\(A(j\omega)=j\omega+\omega_z\)
可以变形为：\(A(j\omega)=\omega_z(1+\frac{j\omega} {\omega_z})\)
其中\(\omega_z\)可以划归进常数因子，我们只需考虑\(A'(\omega)=(1+j\frac{\omega} {z_i})\).有：
\(20\lg A'(\omega)=20\lg \sqrt{1+(\frac\omega{\omega_z})^2}\)
\(\varphi'(\omega)=\tan^{-1}\left(\frac{\omega} {\omega_z}\right)\)
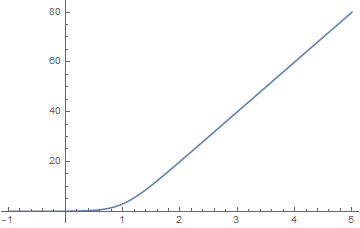
我们观察幅频特性，它并不是一个非常容易画的函数。但是我们感性认识一下，发现它应该近似于一个线性函数。我们取零点为\(-10^1\)，即\(\omega_z=10^1\)，用mathematica 12绘制图像：
1 | |
我们发现它近似于一个与\(x\)轴交于\(1\)点，增长速度为\(20\text{dB}/\)十倍频的直线。
如法炮制，绘制相频曲线：
1 | |
以上两个图的横轴是\(10^x \omega_{zi}\)上面的那个指数，所以你看着是\(0\)的地方，其实对应的是\(1\omega_z\)
于是，我们可以得到近似画法：
极点因子
即： \[ A(\omega)=\frac{1} {j\omega+\omega_p} \]
可以变形为： \[ A(j\omega)=\frac{1} {w_p(j\frac{\omega} {\omega_p}+1)} \] 同理，\(\omega_p^{-1}\)也可以划归为常数因子，则： \[ A'(\omega)=\frac 1 {j\frac \omega {\omega_p}+1} \] 有：
\(20\lg A'(\omega)=-20\lg \sqrt{1+(\frac{\omega} {\omega_p})^2}\)
\(\varphi'(\omega)=-\tan^{-1}(\frac{\omega} {\omega_p})\)
这个其实就是前面一阶零点的相反数，也就不需要再拿软件画图看性质了。这里的\(\omega_p=-p_i\).简化图如下： 
作图的一般流程
首先求出各零、极点，将网络函数写成 \[ H(j\omega)=H_0\frac{(j\omega-z_1)(j\omega-z_2)\cdots(j\omega-z_m)} {(j\omega-p_1)(j\omega-p_2)\cdots(j\omega-p_n)} \] 的形式。
提取各零、极点因子的常数项，把零点和极点转换成\(\omega_z,\omega_p\),把它们都变成\((1+j\frac{\omega} {\omega_z})\)、\(\frac{1} {1+j\frac{\omega} {\omega_p} }\)的形式。这时，有： \[ H(j\omega)=H(0)\frac{(1+j\frac{\omega} {\omega_{z1} })(1+j\frac{\omega} {\omega_{z2} })\cdots(1+j\frac{\omega} {\omega_{zm} })} {(1+j\frac{\omega} {\omega_{p1} })(1+j\frac{\omega} {\omega_{p2} })\cdots(1+j\frac{\omega} {\omega_{pn} })} \] 其中： \[ H(0)=H_0\frac{\prod _{i=1}^m \omega_{zi} } {\prod_{i=1}^n \omega_{p_i} } \]
根据叠加原理，结合上面各个因子的图像画出波特图。
系统稳定性的判断
在6.2 暂态响应和稳态响应中，我们讨论过系统零极点的位置对系统的响应的影响。即：\(H(s)\)的极点如果全部位于左半平面，则系统稳定。当虚轴存在一阶零点时，称为边界稳定或者震荡稳定；当右半平面有极点，或者虚轴上有高阶极点时，称系统不稳定。
首先基于\(H(s)=N/D\)的阶次进行分析。其中\(N\)是\(m\)阶多项式，\(D\)是\(n\)阶多项式。
如果\(m>n\)，系统一定存在一个无穷远点处的极点。基于这个事实，有以下系统稳定的必要条件：
- \(m\leq n\)是系统稳定的必要条件
- \(m>n+1\)时，系统一定不稳定
因此，我们在前面几乎只讨论\(m\leq n\)的系统。
基于分母多项式的根的分布判别
必要条件
- \(D(s)\)的所有系数都同号
- \(D(s)\)不缺项，或者缺全部的奇次或偶次项
上面两个条件是必要条件，只要任一条件不被满足，系统就不是稳定的。但是即使全部满足，系统也不一定稳定。例如： \[ D(s)=2s^3+s^2+3s+9 \]
劳斯判据
劳斯判据就是列劳斯表，然后看第一列是不是全同号。劳斯表是这样列的：
前两行，第一行从前往后是\(a_n,a_{n-2},a_{n-4},\cdots\)，直到下标小于\(0\)；第二行，是\(a_{n-1},a_{n-3},\cdots\)，直到下标小于\(0\)。设劳斯表第\(i\)行第\(j\)列的元素是\(m_{ij}\)，在第三行之后，有： \[ m_{ij}=-\frac{1} {m_{i-1,i} }\begin{vmatrix} m_{i-2,1} & m_{i-2,j+1}\\ m_{i-1,1} & m_{i-1,j+1}\\ \end{vmatrix} \] 如果出现\(0\)，那就把它替换成一个\(\varepsilon>0\)极小量，然后继续算。 我写了个代码来进行这个过程：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84#include <cstdio>
#include <cstring>
#include <cmath>
#include <set>
#include <queue>
#include <stdlib.h>
#include <algorithm>
#define LL long long
#define MAXN 100+10
const double eps = 1e-8;
using namespace std;
double hls(double aa, double ab, double ba, double bb) {
/*
aa ab
ba bb
*/
return aa * bb - ab * ba;
}
double sgn(double x) {
return x > 0.0 ? 1.0 : -1.0;
}
double epsilon = 0.01;
int main() {
int n;
printf("输入多项式的次数：");
scanf("%d", &n);
double a[MAXN], lis[MAXN][MAXN];
printf("从低到高输入系数：");
for (int i = 0; i <= n; ++i)
scanf("%lf", &a[i]);
int lincnt;
for (int i = 1; i <= n + 1; ++i) {
if (i == 1) {
for (int j = 1; (n - (2 * (j - 1)) >= 0); ++j) {
lis[i][j] = a[n - (2 * (j - 1))];
lincnt = j;
}
} else if (i == 2) {
for (int j = 1; j <= lincnt; ++j) {
if (n - (2 * j - 1) >= 0) lis[i][j] = a[n - (2 * j - 1)];
else lis[i][j] = 0;
}
} else {
int flag = 1, j = 1;
for (j = 1; j <= lincnt; ++j) {
lis[i][j] = hls(lis[i - 2][1], lis[i - 2][j + 1], lis[i - 1][1], lis[i - 1][j + 1]) / (-lis[i - 1][1]);
if (fabs(lis[i][j]) < eps) {
if (j == 1)
lis[i][j] = epsilon;
} else {
flag = 0;
}
}
if (flag == 1) {
printf("第 %d 行全为0，系统不稳定，判定结束。\n", i);
return 0;
}
}
}
for (int i = 1; i <= n + 1; ++i) {
printf("\"%d\"", i);
for (int j = 1; j <= lincnt; ++j) {
printf("%+8.2f", lis[i][j]);
}
printf("\n");
}
int f = sgn(lis[1][1]);
for (int i = 2; i <= n + 1; ++i) {
if (sgn(lis[i][1]) != f) {
printf("第 %d 行出现异号，不稳定.\n", i);
return 0;
}
}
printf("稳定。\n");
return 0;
}例如，对于\(s^4+2s^3+8s^2+3s+4\)，输入
1
24
4 3 8 2 1输出：
1
2
3
4
5
6"1" +1.00 +8.00 +4.00
"2" +2.00 +3.00 +0.00
"3" +6.50 +4.00 -0.00
"4" +1.77 +0.00 -0.00
"5" +4.00 -0.00 -0.00
稳定。对于\(2s^4+2s^3+4s^2+4s+5\)，输入
1
24
5 4 4 2 2输出
1
2
3
4
5
6"1" +2.00 +4.00 +5.00
"2" +2.00 +4.00 +0.00
"3" +0.01 +5.00 -0.00
"4" -996.00 +0.00 -0.00
"5" +5.00 -0.00 +0.00
第 4 行出现异号，不稳定.