关于微分方程和系统框图的那些事

昨天做了做作业，发现有通过系统框图写微分方程、和通过微分方程画系统框图这两种题目。初看完全摸不着头脑，但是只要把握\(LTI\)系统的性质就很简单了。

怎么通过系统框图写微分方程？

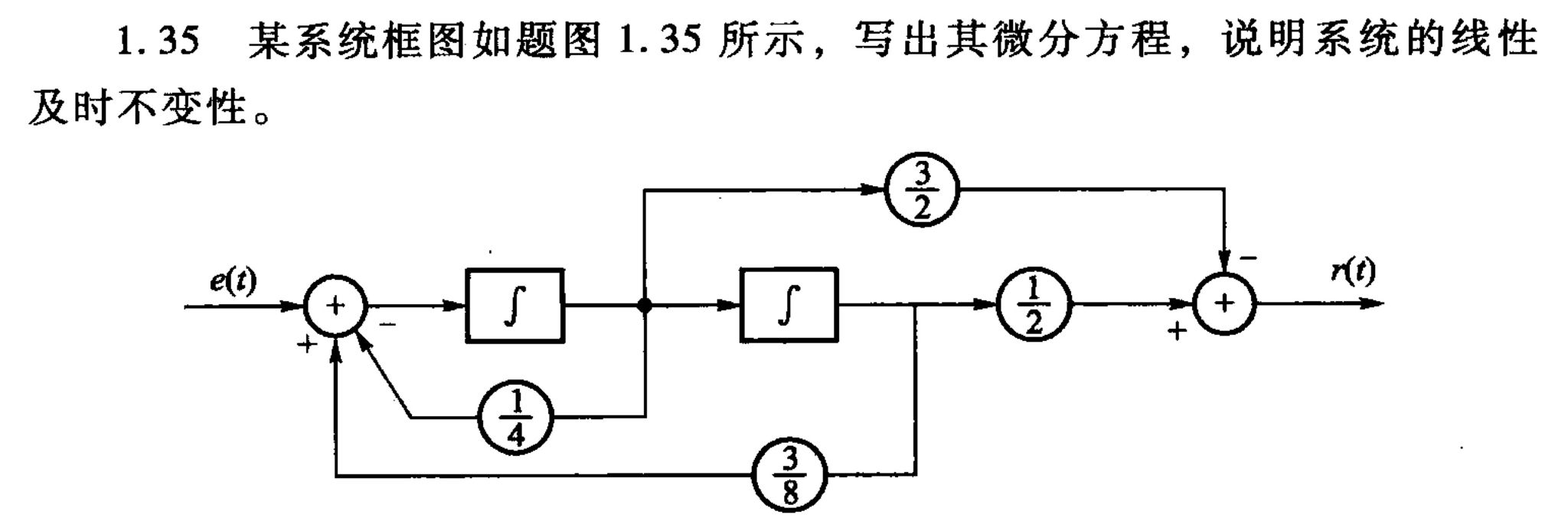
我们很容易想到，首先设一个中间变量\(x(t)\)，这里我把\(x(t)\)放在第二个积分器和\(\frac{1}{2}\)倍乘器中间。那么两个积分器之间的信号就是\(x'(t)\)，第一个积分器前的信号就是\(x''(t)\)，根据两个累加器，我们可以列出方程： \[ \begin{cases} r(t)=-\frac{3}{2}x'(t)+\frac{1}{2}x(t)\\ e(t)+\frac{3}{8}x(t)-\frac{1}{4}x'(t)=x''(t) \end{cases} \] 整理得： \[ \begin{cases} r(t)=-\frac{3}{2}x'(t)+\frac{1}{2}x(t)\\ e(t)=-\frac{3}{8}x(t)+\frac{1}{4}x'(t)+x''(t) \end{cases} \] 那然后怎么消掉\(x(t)\)呢？有人说，线性变换，加加减减就行了呀。没错，非常正确，但是我算不出来。我想了一想，发现了一种方法，可以立刻就把微分方程写出来：只需要把第\(2\)个式子右边的\('x'\)统一换成\('r'\)，写在等号左边，然后把第\(1\)个式子右边的\('x'\)统一换成\('e'\)，写在等号的右边，就大功告成啦！对这个题来说，就是： \[ r''(t)+\frac{1}{4}r'(t)-\frac{3}{8}r(t)=-\frac{3}{2}e'(t)+\frac{1}{2}e(t) \] 这么简单么？只替换两个字符就行了？为啥啊？其实，这利用了\(LTI\)系统的性质。

我们把第二个式子也看作一个线性系统，输入\(e(t)\)，输出\(x(t)\)。那么如果我们把输入改为 \[ \frac{1}{2}e(t)-\frac{3}{2}e'(t) \] 此时这个小系统的输出是什么呢？显然，是 \[ \frac{1}{2}x(t)-\frac{3}{2}x'(t) \] 这是什么呢？结合方程组第一个式子，我们发现这就是\(r(t)\)。

对于第二个式子所代表的,输入\(e\)输出\(x\)的系统 \[ e(t)=-\frac{3}{8}x(t)+\frac{1}{4}x'(t)+x''(t) \] 现在我们输入了\(\frac{1}{2}e(t)-\frac{3}{2}e'(t)\),输出了\(r(t)\)，那么填进去，就有： \[ r''(t)+\frac{1}{4}r'(t)-\frac{3}{8}r(t)=-\frac{3}{2}e'(t)+\frac{1}{2}e(t) \] 完毕。

怎么通过微分方程画系统框图

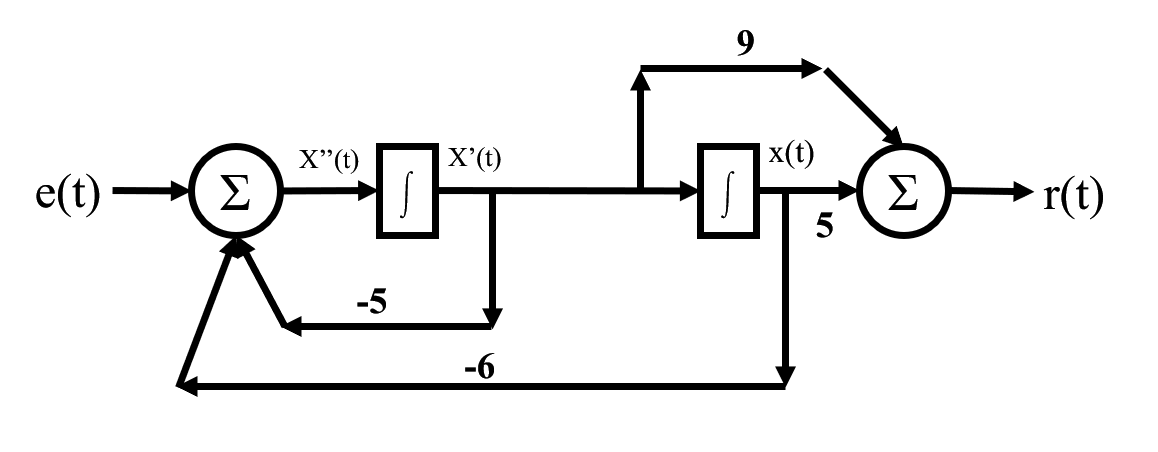
例如： \[ r''(t)+5r'(t)+6r(t)=9e'(t)+5e(t) \] 这个系统相对来说还是比较复杂的。我们遵循上一部分的思路，逆过来思考。

设\(x(t)\)是系统输入为\(e(t)\)时的输出，即： \[ x''(t)+5x'(t)+6x(t)=e(t) \]
这时由于\(LTI\)系统的线性时不变性质（把上面那个式子右边的\(e(t)\)变成\(9e'(t)+5e(t)\)），有： \[ r(t)=9x'(t)+5x(t) \]
把1.中的式子进行一个移项，变成： \[ x''(t)=e(t)-5x'(t)-6x(t) \]
现在可以开始画图了。因为是二阶系统，所以先画2个积分器，标上\(x(t)\),再画上加法器