合成孔径雷达的「斑马图」到底是怎么回事
在合成孔径雷达(以下简称SAR)的波位设计中,经常会遇到一个叫做「斑马图」(或者「菱形图」)的东西,它大概长这样:
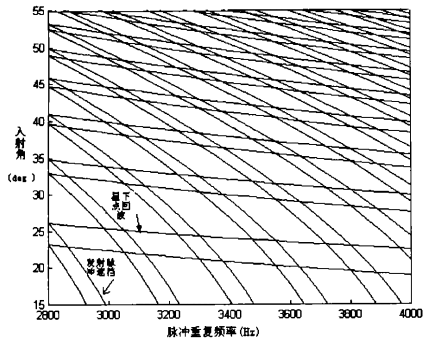
斑马图的横轴是脉冲重复频率,纵轴一般是入射角或者距星下点地面距离。其中有两组曲线,分别表示了星下点回波的干扰和发射信号盲区。对于发射和接收公用一个天线的星载 SAR 系统,由于在任何时刻空中同时有发射脉冲、星下点脉冲和回波必须对 PRF 加以限制,使发射脉冲、星下点脉冲不落在回波窗之中。只有当脉冲重复频率和星下点地面距离的选择在图里的「大菱形区域」里,SAR才能正常工作。如何选择脉冲重复频率或者星下点地面距离,就是所谓的「波位设计」。
我接触到的很多教材都对这个东西的绘制语焉不详,所以在这里我写一下怎么画。画斑马图的关键是几何关系:
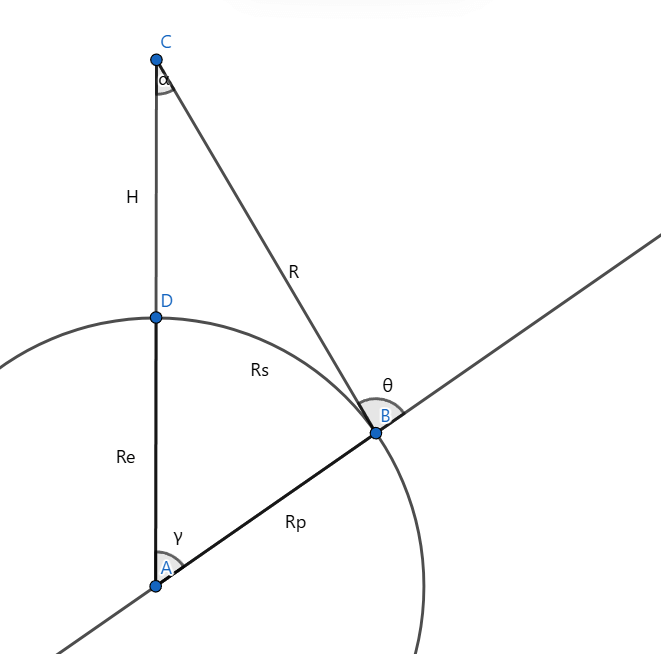
在这个图中,以点
对于一个SAR系统,要绘制其斑马图,还要知道脉冲宽度
绘制发射信号干扰带的斑马图
计算其前后沿回波时间:
假设总共要画
计算对应的最大最小斜距:
计算对应的最大最小视角:
即解三角形
计算对应的最大最小入射角:
即解三角形
由余弦定理:
计算最大最小地距:
由圆弧
由上面的推导,可以看出,
让我们说得再明白一点,也就是说每个
现在的问题是:
回到前面的几何关系:

也就是说,解三角形
过
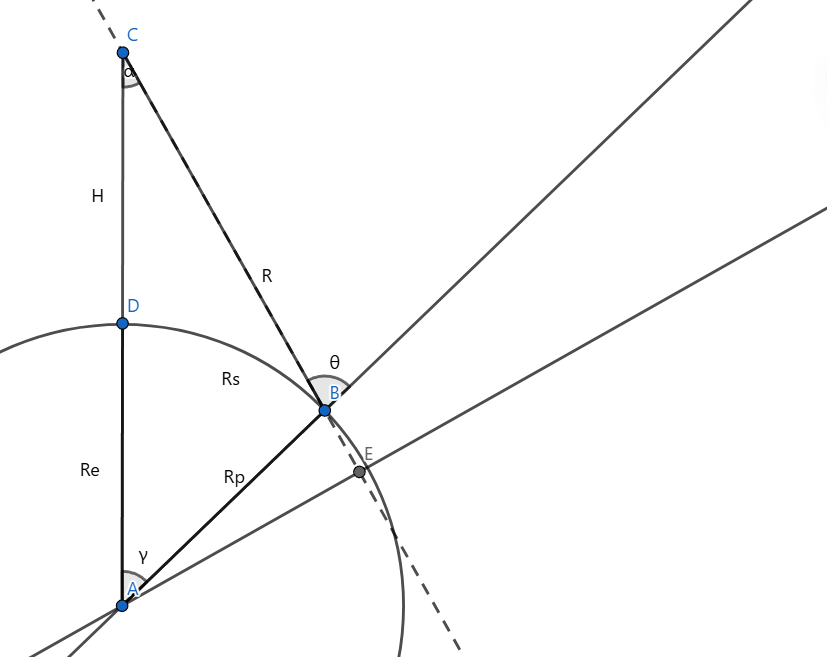
则有:
于是
绘制星下点回波区的斑马图
首先,计算前后沿回波时间
后面的计算和上一部分的完全一样。
关于
算法伪代码


本站的运行成本约为每个月5元人民币,如果您觉得本站有用,欢迎打赏:
