实变泛函·实变函数之章

[toc]

实变函数和泛函分析是一门广度极强的学科，融合了分析、代数、抽代、拓扑等数学各个方面的知识。在学习时要能建立起各个概念之间的联系。

点集

$R^n$中的线性运算、内积和范数

$n$维欧氏空间$R^n$

$R^n$指的是$n$维向量组成的集合： $$R^n=\{(x_1,x_2,\cdots ,x_n):x_i\in R,i=1,2,\cdots n\}$$ 在这个集合上定义加法和数乘： $$\begin{array}{rl}& \mathrm{\forall }x,y\in R^n,\lambda \in R\\ & x+y=(x_1+y_1,x_2+y_2,\cdots ,x_n+y_n)\\ & \lambda x=(\lambda x_1,\lambda x_2,\cdots ,\lambda x_n)\end{array}$$ 其满足所谓的“线性运算八条性质”：对任意的$x,y\in R^n;\lambda ,\mu \in R$

1. $x+y=y+x$
2. $x+y+z=(x+y)+z=x+(y+z)$
3. $$;
4. $$
5. $$
6. $$
7. $$
8. $$

对于$$，定义内积： $$ 内积满足以下三条性质：对于任意的$$，任意的$$，有：

1. 正定性：$$
2. 对称性：$$
3. 对第一变元的线性：
   1. $$
   2. $$

定义了内积的$$维向量空间被称为“内积空间”，也叫“欧几里得空间”.

对于一般的内积空间$$，总成立柯西-施瓦茨不等式： $$ 其中$$，称之为向量的范数。范数满足以下三条性质：

1. 正定性：$$，取到$$当且仅当$$
2. 齐次性：$$
3. 三角不等式：$$

其实，只要$$满足以上三个条件，那么它就可以被称作范数，范数不只有上面所提到的那一种定义。

对三角不等式的证明可以先对式子两边取平方，再运用柯西-施瓦茨不等式。

如果$$且$$ ,则存在实数$$，满足： $$ 这个实数称为两个向量之间的夹角。

最后，我们定义两点间的距离：$$。距离的本质是范数，满足范数的性质。

$$中点列的极限

设$$是$$中的点列，如果$$，称$$收敛于$$，记作： $$ 点列的极限满足以下四条性质：

1. 点列的极限如果存在，那么唯一
2. 收敛点列必定有界
3. $$
4. $$

点列收敛等价于点列的每个分量都收敛（即按分量收敛）。

$$中点集的基本概念和性质

$$，则称集合$$称为以$$为心，$$为半径的“开球”或者“球形邻域”，记作$$.

令$$，称作“闭球”

令$$，称作“去心开球”

若$$，称$$是有界的。否则，称$$是无界的。

点

如果$$，则$$叫做$$的内点，如果$$是$$($$的补集)的内点，那么$$叫做$$的外点。如果$$对$$来说既不是内点，也不是外点，那么$$叫做$$的边界点。

换句话说：以$$为心的任意邻域内都存在属于$$的点，同时也存在不属于$$的点，那么$$叫做$$的边界点。

如果以$$为心的任意球形邻域中都含有$$的无限多个点，那么$$叫做$$的聚点，也叫极限点。聚点的定义可以简化，也就是说，只要以$$为心的任意球形邻域中都含有$$中不同于$$的一个点，那么$$就是$$的聚点。很显然，这两种说法实际上是等价的。还有一种等价的说法：从$$中选出互不相同的点组成点列$$，如果$$，那么$$是$$的聚点。$$中不是聚点的点叫做孤立点。

关于各种点之间的关系，有如下的结论：

1. 内点一定是聚点，外点一定不是聚点
2. 聚点可以是内点，也可以是边界点，但不可能是外点
3. 孤立点一定是边界点
4. 边界点是聚点或孤立点
5. 如果一个点既不是聚点，也不是边界点，那么一定是外点
6. 内点必属于集合，外点必不属于集合，边界点不一定属于集合

我们会发现：聚点不一定在集合内，例子很简单：对于$$

设$$，那么称$$在$$中稠密。稠密等价于以下两个结论：

1. 对$$，总存在$$中的点列收敛于$$。
2. $$中的点要么是$$中的点，要么是$$的聚点。

开集

点集$$的全体内点的集合叫做$$ 的内部，记作$$。如果$$，那么称$$为开集。

几个经典的开集：空集、$$、数轴上的开区间、$$、开球

任意多个开集的并还是开集，有限个开集的交还是开集

闭集

如果$$是开集，那么$$叫做闭集。

几个经典的闭集：数轴上的闭区间、$$的横轴和下半平面、有限个点的集合、开球的补

集合可以既不是开集也不是闭集。

任意个闭集的交还是闭集，有限个闭集的并还是闭集。

点集$$的全体聚点的集合叫做$$的导集，记作$$。如果$$，那么$$叫做$$的闭包。

如果$$是闭集，那么它的闭包是它自己。

内部是含于一个集合的最大开集，闭包是包含一个集合的最小闭集。

$$中的基本定理

我们在学实数的时候经常提“六大定理”，即：

1. 确界存在定理
2. 单调数列收敛定理
3. 有界数列必有收敛子列
4. 柯西收敛准则
5. 闭区间套定理
6. 有限覆盖定理

在$$中，前两个定理不再成立，后面的继续成立。

• $$中的有界点列必有收敛子列，也就是：任何无穷点集都含有聚点

• 如果$$是$$中的点列，如果$$，称$$是基本列。“是基本列”和“收敛”等价。

• 设$$是一个闭集列，都不是空集，而且：

  • 后一项是前一项的子列
  • $$

  那么存在唯一的$$，其中$$。

• 设$$是$$中的一个开集族，如果$$，称$$是$$的一个开覆盖。$$中的有界闭集的任意一个开覆盖都有有限子覆盖

距离

点$$和集合$$的距离为： $$ 意思就是点到集合中每个点的距离的下确界

两个集合之间的距离为： $$ 意思就是从集合里面任选两个点，它们之间的距离的下确界

有以下结论：

1. 如果A是非空闭集，则$$
2. 如果AB是非空闭集，则$$
3. $$是不相交的非空闭集，则存在$$上的连续函数，使得
   1. $$
   2. $$；$$

康托尔（Cantor）三分集

把$$三等分，去掉中间的一部分，再把左右两个剩下的三等分，再各自去掉中间的一部分，重复无限次，剩下来的集合就是Cantor三分集（P）。

它：

1. 是闭集，完备集
2. 没有内点
3. 是疏朗集，即$$(闭包)没有内点
4. 基数是连续势
5. 测度为零，外测度也为零

康托尔函数$$：把在构造康托尔集的过程中第$$次去掉的$$个开区间上依次取值为 $$ 规定$$

康托尔函数是$$上的单调不减连续函数。

测度论

测度是“长度”、“面积”概念的扩展。

集合的测度$$应当满足：

1. 非负性

2. 正则性：若$$，则$$

3. 可数可加性：如果集合$$都有测度且两两不交，那么： $$

这里主要讨论勒贝格测度。在定义测度时，先定义勒贝格外测度，然后在其基础上诱导出一个可测集合类，在其上的外测度就是一种期望的测度。

外测度

对于$$的子集$$，定义非负广义函数： $$ 开矩体是$$个开区间的直积，其体积为每个开区间的长度之积。

外测度有以下性质：

1. 非负性

2. 单调性：如果$$，则$$

3. 次可数可加性：如果集合$$都有测度且两两不交，那么： $$

4. 平移不变性： $$ 其中$$

可测集

定义，如果$$： $$ 则称$$是勒贝格可测集，简称为可测集。此时$$称为$$的测度，记作$$。这个等式叫做卡特西奥多里条件。

这个条件可以等价于： $$ 设$$上的可测集所构成的集族称为M，则：

1. 空集属于M
2. 如果$$可测，那么$$可测
3. 如果$$，则它们的并、交、差都是可测
4. 可测集的有限并也可测，而且满足可列可加

区间可测，凡是开集或闭集都可测，外测度为零的集合可测且测度为零

零测集的子集、至多可数个零测集的并也是零测集。

不可测集

存在不可测集。

可测函数

可测函数的定义和性质

设$$是定义在可测集$$上的广义实值函数，若$$，$$（即$$）都是可测集，则称$$为可测函数。

以下条件相互等价：

• $$是可测函数，即$$可测
• $$可测
• $$可测
• $$可测

如果$$在可测集$$上是可测函数，那么在$$的每个可测子集上也是可测函数。

如果$$，其中每一个$$都是可测集而且$$在其上可测，那么$$在$$上可测。

可测函数类关于确界、上下极限封闭。即：如果$$都是可测集$$上的函数，那么$$都可测。

可测函数类关于加、减、乘、除、数乘、绝对值封闭。

如果$$是一个和集合$$中元素$$有关的命题，如果存在一个$$的零测子集$$，使得$$在$$上恒成立，称$$在$$上几乎处处成立，记作$$

如果$$都是$$上的广义实值函数，且$$，那么$$可测是$$可测的充要条件。

下面定义三种函数：

1. 设$$的一个子集$$，称： $$ 为$$上的特征函数。如果$$可测，那么它的特征函数可测。

2. 如果$$的定义域$$可以分为有限个不相交的集合$$，且$$在每个$$上取常值$$，那么称$$是$$上的简单函数。（简单理解：取有限个实数）

3. 如果在简单函数的定义的基础上，每个$$都是矩体，称$$为阶梯函数。

可测函数和简单函数的关系(简单函数逼近定理)

如果$$是可测集$$上的非负可测函数，当且仅当存在非负可测渐升简单函数列$$，使得： $$ 如果$$在$$上有界，那么上述收敛是一致的。

事实上，作简单函数列$$，使得： $$ 其中 $$ 即满足上述定理的要求。

如果$$是可测集$$上的可测函数，当且仅当存在可测的简单函数列$$，满足：

1. $$
2. $$

如果$$在$$上有界，那么上述收敛是一致的。

在证明时，可以把$$分解成正负部之差，利用前面关于非负函数的定理，令 $$

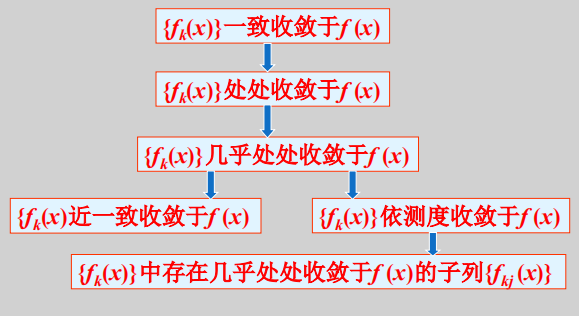
可测函数的收敛

设$$都是定义在$$上的可测函数，有：

1. 处处收敛：$$当$$时，有：$$，记作 $$

2. 几乎处处收敛：存在一个零测集，使得$$在$$中除了这个零测集以外的点上收敛于$$

3. 一致收敛：$$当$$时，有：$$。一致收敛等价于： $$

有Egoroff（叶洛果夫）定理：设$$，如果$$在$$上几乎处处收敛，那么对于任意的$$，有$$的可测子集$$，使得$$在$$上一致收敛。也就是说，几乎处处收敛的函数列是“近一致收敛”的。

例如，对于函数列$$，$$，其处处收敛于 $$ 因 $$ 不趋向于$$，所以它不是一致收敛的。然而只要去掉任意小的区域，把$$变成$$，那么就一致收敛了。

其实还有比几乎处处收敛更弱的收敛，叫做依测度收敛。如果$$是可测集$$上的几乎处处有限的函数，如果对任意$$，有： $$ 即：$$与$$的差值比$$大的集合的测度趋向于0，那么说$$依测度收敛于$$。

几乎处处收敛比依测度收敛更强，是因为几乎处处有限可以推出依测度收敛，反之不然。

如果函数列依测度收敛，那么存在函数列的子列$$几乎处处收敛，这叫做Riesz定理。

如果$$是可测集$$上的几乎处处有限的函数，$$，使得$$在闭集$$上连续，这叫做鲁津定理。

有关可测函数的常见结论和各种收敛的关系总结如下：

• 可测函数与零测集无关.
• 可测函数是简单函数列处处收敛的极限.(当可测函数有界时, 可做到一致收敛)
• 可测函数关于一些运算的封闭性.
• 可测集 $$ 上的连续函数是可测的.
• 可测集 $$ 上的简单函数是可测的.
• $$ 中可测集 $$ 上的单调函数是可测的.

各种收敛

勒贝格积分

首先我们从简单函数出发：假设$$是$$上的非负简单函数，在$$上取值$$，且$$。也就是说： $$ 那么定义$$在$$上的勒贝格积分（下简称为L积分）为： $$ 根据简单函数逼近定理，我们可以把这个定义扩展到非负可测函数上：如果$$是$$上的非负可测函数，那么定义$$的L积分： $$ 其中$$是$$上的非负可测简单函数。如果有： $$ 就称$$是$$上可积的。

进一步，因为每个可测函数都可以分解成两个非负可测函数的差（即正部和负部），有： $$ 定义可测函数上的L积分： $$

L积分的性质

L积分的条件

以下，记$$为在$$上L可积的函数构成的集合。

1. 【必要条件】：$$在$$上几乎处处有界
2. 【充分条件】：$$是$$上的有界可测函数，$$，则$$
3. 【充分条件】：$$是$$上的可测函数，$$，则$$

L积分的基本性质

1. 线性，保序性

   略，和黎曼积分（以下简称R积分）相同

2. 有限可加性

   如果$$，那么$$在$$的子集上也L可积。

   如果$$可测，那么 $$

3. 集合意义

   如果$$是$$上的非负实值函数，称： $$ 为$$在$$上的下方图形，如果$$在$$上可测，那么他的下方图形在$$上也可测，有： $$ 如果$$可测，则$$在$$上可测，$$也 可测，且也有上面的结论

L积分的特殊性质

1. 零测集上任何函数L积分为零，更进一步，如果两个函数只在一个零测集上有区别，那么这两个函数的L积分相等

2. 函数$$L可积和其绝对值$$L可积等价，且积分的绝对值不大于绝对值的积分

3. 绝对连续性：如果$$，则$$，有： $$

4. 如果一个函数R可积，那么它L可积，且两个积分的值相等。

   这说明，R积分的有关问题，可以转换为L积分，再利用马上就要说明的L积分的优良性质完成 。

L积分的优良性质

【勒贝格收敛控制定理】如果$$是$$上的可测函数列，且：

1. $$
2. $$

那么，$$，且积分和极限可以交换次序，有： $$

相比之下，黎曼积分需要函数列一致收敛，才能交换顺序。一致收敛是一个非常强的条件。

推论：如果$$是$$上的可测函数列，且：

1. $$
2. $$
3. $$

那么，$$，且积分和极限可以交换次序，有： $$ 推论：设$$，且有： $$ 则：

1. $$几乎处处收敛

2. 其和函数$$，且 $$

【例】求 $$

【解】因为原函数列不一致收敛，因此需要用L积分。

验证勒贝格收敛控制定理： $$

则有： $$

有时候，问题中并不显式地出现极限、求和符号，但是可以通过把被积分展开成级数的和，再求解：

【例】 $$ 【解】

首先展开成级数： $$

我们发现这不是一致收敛的，但是没关系，我们有勒贝格积分： $$

---

本站的运行成本约为每个月5元人民币，如果您觉得本站有用，欢迎打赏：